![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
Next: Chapter Notes
Up: 11 Hypercube Algorithms
Previous: 11.5 Summary
-
Execute the hypercube summation algorithm by hand for N=8, and
satisfy yourself that you obtain the correct answer.
-
Use Equations 11.1 and 11.2 to identify problem size,
processor count, and machine parameter regimes in which each of the
two vector reduction algorithms of Section 11.2 will be
more efficient.
-
Implement the hybrid vector reduction algorithm described in
Section 11.2. Use empirical studies to determine the
vector length at which the switch from recursive halving to exchange
algorithm should occur. Compare the performance of this algorithm
with pure recursive halving and exchange algorithms.
-
A variant of the parallel mergesort algorithm performs just
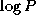 compare-exchange operations and then switches to a parallel
bubblesort [174]. In the bubblesort phase, tasks are
connected in a logical ring and each task performs compare-exchange
operations with its neighbors until a global reduction shows that no
exchanges occurred. Design an implementation of this algorithm, using
hypercube and ring structures as building blocks.
compare-exchange operations and then switches to a parallel
bubblesort [174]. In the bubblesort phase, tasks are
connected in a logical ring and each task performs compare-exchange
operations with its neighbors until a global reduction shows that no
exchanges occurred. Design an implementation of this algorithm, using
hypercube and ring structures as building blocks.
-
Implement the modified parallel mergesort of Exercise 4.
Compare its performance with regular parallel mergesort for different
input sequences and for a variety of P
and N
.
-
Extend Equations 11.3 and 11.4 to account
for bandwidth limitations in a one-dimensional mesh.
-
Modify the performance models developed for the convolution algorithm
in Section 4.4 to reflect the use of the hypercube-based
transpose. Can the resulting algorithms ever provide superior
performance?
-
Use the performance models given in Section 11.2 for the
simple and recursive halving vector reduction algorithms to determine
situations in which each algorithm would give superior performance.
-
Design and implement a variant of the vector sum algorithm that does
not require the number of tasks to be an integer power of 2.
-
Develop a CC++
, Fortran M, or MPI implementation of a ``hypercube
template.'' Use this template to implement simple reduction, vector
reduction, and broadcast algorithms. Discuss the techniques that you
used to facilitate reuse of the template.
-
Implement a ``torus template'' and use this together with the template
developed in Exercise 10 to implement the finite
difference computation of Section 4.2.2.
-
Develop a performance model for a 2-D matrix multiplication algorithm
that uses the vector broadcast algorithm of Section 11.2
in place of the tree-based broadcast assumed in
Section 4.6.1. Discuss the advantages and disadvantages
of this algorithm.
-
Implement both the modified matrix multiplication algorithm of
Exercise 12 and the original algorithm of
Section 4.6.1, and compare their performance.
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)
Next: Chapter Notes
Up: 11 Hypercube Algorithms
Previous: 11.5 Summary
© Copyright 1995 by Ian Foster
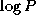 compare-exchange operations and then switches to a parallel
bubblesort [174]. In the bubblesort phase, tasks are
connected in a logical ring and each task performs compare-exchange
operations with its neighbors until a global reduction shows that no
exchanges occurred. Design an implementation of this algorithm, using
hypercube and ring structures as building blocks.
compare-exchange operations and then switches to a parallel
bubblesort [174]. In the bubblesort phase, tasks are
connected in a logical ring and each task performs compare-exchange
operations with its neighbors until a global reduction shows that no
exchanges occurred. Design an implementation of this algorithm, using
hypercube and ring structures as building blocks.
![[DBPP]](pictures/asm_color_tiny.gif)





![[Search]](pictures/search_motif.gif)