BASIC interpreter
The application described in this section is a program interpreter for
Basic. Thus, it is a program that can run other programs written in
Basic. Of course, we will only deal with a restricted language,
which contains the following commands:
-
PRINT expression
| |
Prints the result of the evaluation of the expression. |
- INPUT variable
| |
Prints a prompt (?), reads an integer typed in by the
user, and assigns its value to the variable. |
- LET variable = expression
| |
Assigns the result of the evaluation of expression to the variable. |
- GOTO line number
| |
Continues execution at the given line. |
- IF condition THEN line number
| |
Continues execution at the given line if the condition is true. |
- REM any string
Every line of a Basic program is labelled with a line number, and
contains only one command. For instance, a program that computes and
then prints the factorial of an integer given by the user is written:
5 REM inputting the argument
10 PRINT " factorial of:"
20 INPUT A
30 LET B = 1
35 REM beginning of the loop
40 IF A <= 1 THEN 80
50 LET B = B * A
60 LET A = A - 1
70 GOTO 40
75 REM prints the result
80 PRINT B
We also wish to write a small text editor, working as a toplevel interactive
loop. It should be able to add new lines, display a program, execute
it, and display the result.
Execution of the program is started with the
RUN command. Here is an example of the evaluation of this
program:
> RUN
factorial of: ? 5
120
The interpreter is implemented in several distinct parts:
- Description of the abstract syntax
- : describes the definition of data
types to represent Basic programs, as well as their components
(lines, commands, expressions, etc.).
- Program pretty printing
- : consists of transforming the
internal representation of Basic programs to strings, in order
to display them.
- Lexing and parsing
- : accomplish the inverse
transformation, that is, transform a string into the internal
representation of a Basic program (the abstract syntax).
- Evaluation
- : is the heart of the interpreter. It controls
and runs the program. As we will see, functional languages, such as
Objective CAML, are particularly well adapted for this kind of problem.
- Toplevel interactive loop
- : glues together all the previous parts.
Abstract syntax
Figure 6.2 introduces the concrete syntax, as a BNF
grammar, of the Basic we will implement. This kind of description
for language syntaxes is described in chapter 11,
page ??.
| Unary_Op |
::= |
- | ! |
| Binary_Op |
::= |
+ | - | * | / |
% |
| |
| |
= | < | > | <= |
>= | <> |
| |
| |
& | ' | ' |
| Expression |
::= |
integer |
| |
| |
variable |
| |
| |
"string" |
| |
| |
Unary_Op Expression |
| |
| |
Expression Binary_Op Expression |
| |
| |
( Expression ) |
| Command |
::= |
REM string |
| |
| |
GOTO integer |
| |
| |
LET variable = Expression |
| |
| |
PRINT Expression |
| |
| |
INPUT variable |
| |
| |
IF Expression THEN integer |
| |
| Line |
::= |
integer Command |
| |
| Program |
::= |
Line |
| |
| |
Line Program |
| |
| Phrase |
::= |
Line | RUN | LIST | END |
Figure 6.2: BASIC Grammar.
We can see that the way expressions are defined does not ensure that a
well formed expression can be evaluated. For instance, 1+"hello" is an expression, and yet it is not possible to evaluate
it. This deliberate choice lets us simplify both the abstract syntax
and the parsing of the Basic language. The price to pay for
this choice is that a syntactically correct Basic program may generate
a runtime error because of a type mismatch.
Defining Objective CAML data types for this abstract syntax is easy,
we simply translate the concrete syntax into a sum type:
# type unr_op = UMINUS | NOT ;;
# type bin_op = PLUS | MINUS | MULT | DIV | MOD
| EQUAL | LESS | LESSEQ | GREAT | GREATEQ | DIFF
| AND | OR ;;
# type expression =
ExpInt of int
| ExpVar of string
| ExpStr of string
| ExpUnr of unr_op * expression
| ExpBin of expression * bin_op * expression ;;
# type command =
Rem of string
| Goto of int
| Print of expression
| Input of string
| If of expression * int
| Let of string * expression ;;
# type line = { num : int ; cmd : command } ;;
# type program = line list ;;
We also define the abstract syntax for the commands for the small
program editor:
# type phrase = Line of line | List | Run | PEnd ;;
It is convenient to allow the programmer to skip some parentheses in
arithmetic expressions. For instance, the expression 1+3*4 is
usually interpreted as 1+(3*4). To this end, we associate an integer
with each operator of the language:
# let priority_uop = function NOT -> 1 | UMINUS -> 7
let priority_binop = function
MULT | DIV -> 6
| PLUS | MINUS -> 5
| MOD -> 4
| EQUAL | LESS | LESSEQ | GREAT | GREATEQ | DIFF -> 3
| AND | OR -> 2 ;;
val priority_uop : unr_op -> int = <fun>
val priority_binop : bin_op -> int = <fun>
These integers indicate the priority of the operators. They
will be used to print and parse programs.
Program pretty printing
To print a program, one needs to be able to convert abstract syntax
program lines into strings.
Converting operators is easy:
# let pp_binop = function
PLUS -> "+" | MULT -> "*" | MOD -> "%" | MINUS -> "-"
| DIV -> "/" | EQUAL -> " = " | LESS -> " < "
| LESSEQ -> " <= " | GREAT -> " > "
| GREATEQ -> " >= " | DIFF -> " <> " | AND -> " & " | OR -> " | "
let pp_unrop = function UMINUS -> "-" | NOT -> "!" ;;
val pp_binop : bin_op -> string = <fun>
val pp_unrop : unr_op -> string = <fun>
Expression printing needs to take into account operator priority to
print as few parentheses as possible. For instance, parentheses are
put around a subexpression at the right of an operator only if the
subexpression's main operator has a lower priority that the main
operator of the whole expression. Also, arithmetic operators are
left-associative, thus the expression 1-2-3 is interpreted as
(1-2)-3.
To deal with this, we use two auxiliary functions ppl and
ppr to print left and right subtrees, respectively. These
functions take two arguments: the tree to print and the priority of
the enclosing operator, which is used to decide if parentheses are
necessary. Left
and right subtrees are distinguished to deal with associativity. If
the current operator priority is the same than the enclosing operator
priority, left trees do not need parentheses whereas right ones may
require them, as in 1-(2-3) or 1-(2+3).
The initial tree is taken as a left subtree with minimal priority
(0).
The expression pretty printing function pp_expression is:
# let parenthesis x = "(" ^ x ^ ")";;
val parenthesis : string -> string = <fun>
# let pp_expression =
let rec ppl pr = function
ExpInt n -> (string_of_int n)
| ExpVar v -> v
| ExpStr s -> "\"" ^ s ^ "\""
| ExpUnr (op,e) ->
let res = (pp_unrop op)^(ppl (priority_uop op) e)
in if pr=0 then res else parenthesis res
| ExpBin (e1,op,e2) ->
let pr2 = priority_binop op
in let res = (ppl pr2 e1)^(pp_binop op)^(ppr pr2 e2)
(* parenthesis if priority is not greater *)
in if pr2 >= pr then res else parenthesis res
and ppr pr exp = match exp with
(* right subtrees only differ for binary operators *)
ExpBin (e1,op,e2) ->
let pr2 = priority_binop op
in let res = (ppl pr2 e1)^(pp_binop op)^(ppr pr2 e2)
in if pr2 > pr then res else parenthesis res
| _ -> ppl pr exp
in ppl 0 ;;
val pp_expression : expression -> string = <fun>
Command pretty printing uses the expression pretty printing
function. Printing a line consists of printing the line number before
the command.
# let pp_command = function
Rem s -> "REM " ^ s
| Goto n -> "GOTO " ^ (string_of_int n)
| Print e -> "PRINT " ^ (pp_expression e)
| Input v -> "INPUT " ^ v
| If (e,n) -> "IF "^(pp_expression e)^" THEN "^(string_of_int n)
| Let (v,e) -> "LET " ^ v ^ " = " ^ (pp_expression e) ;;
val pp_command : command -> string = <fun>
# let pp_line l = (string_of_int l.num) ^ " " ^ (pp_command l.cmd) ;;
val pp_line : line -> string = <fun>
Lexing
Lexing and parsing do the inverse transformation of
printing, going from a string to a syntax tree. Lexing
splits the text of a command line into independent lexical units
called lexemes, with Objective CAML type:
# type lexeme = Lint of int
| Lident of string
| Lsymbol of string
| Lstring of string
| Lend ;;
A particular lexeme denotes the end of an expression: Lend.
It is not present in the text of the expression, but is created by the
lexing function (see the lexer function, page
??).
The string being lexed is kept in a record that contains a mutable
field indicating the position after which lexing has not been
done yet. Since the size of the string is used several times and does
not change, it is also stored in the record:
# type string_lexer = {string:string; mutable current:int; size:int } ;;
This representation lets us define the lexing of a string as the
application of a function to a value of type string_lexer
returning a value of type lexeme. Modifying the current
position in the string is done as a side effect.
# let init_lex s = { string=s; current=0 ; size=String.length s } ;;
val init_lex : string -> string_lexer = <fun>
# let forward cl = cl.current <- cl.current+1 ;;
val forward : string_lexer -> unit = <fun>
# let forward_n cl n = cl.current <- cl.current+n ;;
val forward_n : string_lexer -> int -> unit = <fun>
# let extract pred cl =
let st = cl.string and pos = cl.current in
let rec ext n = if n<cl.size && (pred st.[n]) then ext (n+1) else n in
let res = ext pos
in cl.current <- res ; String.sub cl.string pos (res-pos) ;;
val extract : (char -> bool) -> string_lexer -> string = <fun>
The following functions extract a lexeme from the string and modify
the current position. The two functions extract_int and
extract_ident extract an integer and an identifier,
respectively.
# let extract_int =
let is_int = function '0'..'9' -> true | _ -> false
in function cl -> int_of_string (extract is_int cl)
let extract_ident =
let is_alpha_num = function
'a'..'z' | 'A'..'Z' | '0' .. '9' | '_' -> true
| _ -> false
in extract is_alpha_num ;;
val extract_int : string_lexer -> int = <fun>
val extract_ident : string_lexer -> string = <fun>
The lexer function uses the two previous functions to extract
a lexeme.
# exception LexerError ;;
exception LexerError
# let rec lexer cl =
let lexer_char c = match c with
' '
| '\t' -> forward cl ; lexer cl
| 'a'..'z'
| 'A'..'Z' -> Lident (extract_ident cl)
| '0'..'9' -> Lint (extract_int cl)
| '"' -> forward cl ;
let res = Lstring (extract ((<>) '"') cl)
in forward cl ; res
| '+' | '-' | '*' | '/' | '%' | '&' | '|' | '!' | '=' | '(' | ')' ->
forward cl; Lsymbol (String.make 1 c)
| '<'
| '>' -> forward cl;
if cl.current >= cl.size then Lsymbol (String.make 1 c)
else let cs = cl.string.[cl.current]
in ( match (c,cs) with
('<','=') -> forward cl; Lsymbol "<="
| ('>','=') -> forward cl; Lsymbol ">="
| ('<','>') -> forward cl; Lsymbol "<>"
| _ -> Lsymbol (String.make 1 c) )
| _ -> raise LexerError
in
if cl.current >= cl.size then Lend
else lexer_char cl.string.[cl.current] ;;
val lexer : string_lexer -> lexeme = <fun>
The lexer function is very simple: it matches the current
character of a string and, based on its value, extracts the
corresponding lexeme and modifies the current position to the start of
the next lexeme. The code is simple because, for all characters except
two, the current character defines which lexeme to extract. In the
more complicated cases of '<', we need to look at the next
character, which might be a '=' or a '>', producing two different
lexemes. The same problem arises with '>'.
Parsing
The only difficulty in parsing our language comes from expressions.
Indeed, knowing the beginning of an expression is not enough to know
its structure. For instance, having parsed the beginning of an
expression as being 1+2+3, the resulting syntax tree for this part
depends on the rest of the expression: its structure is different when
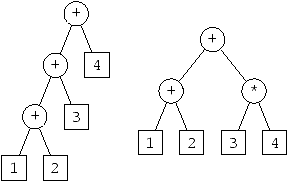
it is followed by +4 or *4 (see figure 6.3).
Figure 6.3: Basic: abstract syntax tree examples
.
However, since the tree structure for 1+2 is the same in both cases,
it can be built. As the position of +3 in the structure is not fully
known, it is temporarily stored.
To build the abstract syntax tree, we use a pushdown automaton
similar to the one built by yacc (see page
??). Lexemes are read one by one and put
on a stack until there is enough information to build the
expression. They are then removed from the stack and replaced by the
expression. This latter operation is called reduction.
The stack elements have type:
# type exp_elem =
Texp of expression (* expression *)
| Tbin of bin_op (* binary operator *)
| Tunr of unr_op (* unary operator *)
| Tlp (* left parenthesis *) ;;
Right parentheses are not stored on the stack as only left parentheses
matter for reduction.
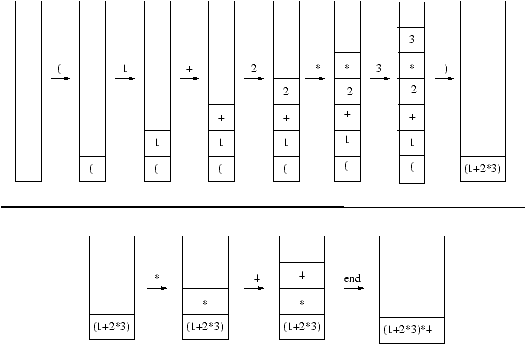
Figure 6.4 illustrates the way the stack is used to
parse the expression (1+2*3)+4. The character above the arrow is the
current character of the string.
Figure 6.4: Basic: abstract syntax tree construction
example
.
We define an exception for syntax errors.
# exception ParseError ;;
The first step consists of transforming symbols into operators:
# let unr_symb = function
"!" -> NOT | "-" -> UMINUS | _ -> raise ParseError
let bin_symb = function
"+" -> PLUS | "-" -> MINUS | "*" -> MULT | "/" -> DIV | "%" -> MOD
| "=" -> EQUAL | "<" -> LESS | "<=" -> LESSEQ | ">" -> GREAT
| ">=" -> GREATEQ | "<>" -> DIFF | "&" -> AND | "|" -> OR
| _ -> raise ParseError
let tsymb s = try Tbin (bin_symb s) with ParseError -> Tunr (unr_symb s) ;;
val unr_symb : string -> unr_op = <fun>
val bin_symb : string -> bin_op = <fun>
val tsymb : string -> exp_elem = <fun>
The reduce function implements stack reduction. There are two
cases to consider, whether the stack starts with:
-
an expression followed by a unary operator,
-
an expression followed by a binary operator and an expression.
Moreover, reduce takes an argument indicating the minimal
priority that an operator should have to trigger reduction. To avoid
this reduction condition, it suffices to give the minimal value, zero,
as the priority.
# let reduce pr = function
(Texp e)::(Tunr op)::st when (priority_uop op) >= pr
-> (Texp (ExpUnr (op,e)))::st
| (Texp e1)::(Tbin op)::(Texp e2)::st when (priority_binop op) >= pr
-> (Texp (ExpBin (e2,op,e1)))::st
| _ -> raise ParseError ;;
val reduce : int -> exp_elem list -> exp_elem list = <fun>
Notice that expression elements are stacked as they are read. Thus it
is necessary to swap them when they are arguments of a binary
operator.
The main function of our parser is stack_or_reduce that,
according to the lexeme given in argument, puts it on the stack or
triggers a reduction.
# let rec stack_or_reduce lex stack = match lex , stack with
Lint n , _ -> (Texp (ExpInt n))::stack
| Lident v , _ -> (Texp (ExpVar v))::stack
| Lstring s , _ -> (Texp (ExpStr s))::stack
| Lsymbol "(" , _ -> Tlp::stack
| Lsymbol ")" , (Texp e)::Tlp::st -> (Texp e)::st
| Lsymbol ")" , _ -> stack_or_reduce lex (reduce 0 stack)
| Lsymbol s , _
-> let symbol =
if s<>"-" then tsymb s
(* remove the ambiguity of the ``-'' symbol *)
(* according to the last exp element put on the stack *)
else match stack
with (Texp _)::_ -> Tbin MINUS
| _ -> Tunr UMINUS
in ( match symbol with
Tunr op -> (Tunr op)::stack
| Tbin op ->
( try stack_or_reduce lex (reduce (priority_binop op)
stack )
with ParseError -> (Tbin op)::stack )
| _ -> raise ParseError )
| _ , _ -> raise ParseError ;;
val stack_or_reduce : lexeme -> exp_elem list -> exp_elem list = <fun>
Once all lexemes are defined and stacked, the function
reduce_all builds the abstract syntax tree with the elements
remaining in the stack. If the expression being parsed is well formed,
only one element should remain in the stack, containing the tree for
this expression.
# let rec reduce_all = function
| [] -> raise ParseError
| [Texp x] -> x
| st -> reduce_all (reduce 0 st) ;;
val reduce_all : exp_elem list -> expression = <fun>
The parse_exp function is the main expression parsing
function. It reads a string, extracts its lexemes and passes them to the
stack_or_reduce function. Parsing stops when the current
lexeme satisfies a predicate that is given as an argument.
# let parse_exp stop cl =
let p = ref 0 in
let rec parse_one stack =
let l = ( p:=cl.current ; lexer cl)
in if not (stop l) then parse_one (stack_or_reduce l stack)
else ( cl.current <- !p ; reduce_all stack )
in parse_one [] ;;
val parse_exp : (lexeme -> bool) -> string_lexer -> expression = <fun>
Notice that the lexeme that made the parsing stop is not used to build
the expression. It is thus necessary to modify the current position to
its beginning (variable p) to parse it later.
We can now parse a command line:
# let parse_cmd cl = match lexer cl with
Lident s -> ( match s with
"REM" -> Rem (extract (fun _ -> true) cl)
| "GOTO" -> Goto (match lexer cl with
Lint p -> p
| _ -> raise ParseError)
| "INPUT" -> Input (match lexer cl with
Lident v -> v
| _ -> raise ParseError)
| "PRINT" -> Print (parse_exp ((=) Lend) cl)
| "LET" ->
let l2 = lexer cl and l3 = lexer cl
in ( match l2 ,l3 with
(Lident v,Lsymbol "=") -> Let (v,parse_exp ((=) Lend) cl)
| _ -> raise ParseError )
| "IF" ->
let test = parse_exp ((=) (Lident "THEN")) cl
in ( match ignore (lexer cl) ; lexer cl with
Lint n -> If (test,n)
| _ -> raise ParseError )
| _ -> raise ParseError )
| _ -> raise ParseError ;;
val parse_cmd : string_lexer -> command = <fun>
Finally, we implement the function to parse commands typed by the
user:
# let parse str =
let cl = init_lex str
in match lexer cl with
Lint n -> Line { num=n ; cmd=parse_cmd cl }
| Lident "LIST" -> List
| Lident "RUN" -> Run
| Lident "END" -> PEnd
| _ -> raise ParseError ;;
val parse : string -> phrase = <fun>
Evaluation
A Basic program is a list of lines. Execution starts at the first
line. Interpreting a program line consists of executing the task
corresponding to its command. There are three different kinds of
commands: input-output (PRINT and INPUT), variable
declaration or modification (LET), and flow control
(GOTO and IF...THEN). Input-output commands interact
with the user and use the corresponding Objective CAML functions.
Variable declaration and modification commands need to know how to
compute the value of an arithmetic expression and the memory
location to store the result. Expression evaluation returns an
integer, a boolean, or a string. Their type is value.
# type value = Vint of int | Vstr of string | Vbool of bool ;;
Variable declaration should allocate some memory to store the
associated value. Similarly, variable modification requires the
modification of the associated value. Thus, evaluation of a Basic
program uses an environment that stores the association
between a variable name and its value. It is represented by an
association list of tuples (name,value):
# type environment = (string * value) list ;;
The variable name is used to access its value. Variable modification
modifies the association.
Flow control commands, conditional or unconditional, specify the
number of the next line to execute. By default, it is the next
line. To do this, it is necessary to remember
the number of the current line.
The list of commands representing the program being edited under
the toplevel is not an efficient data structure for running the
program. Indeed, it is then necessary to look at the whole list of
lines to find the line indicated by a flow control command
(If and goto). Replacing the list of lines with an array
of commands allows direct access to the command following a
flow control command, using the array index instead of the line
number in the flow control command. This solution requires some
preprocessing called assembly before executing a RUN
command. For reasons that will be detailed shortly, a program
after assembly is not represented as an array of commands but as an
array of lines:
# type code = line array ;;
As in the calculator example of previous chapters, the interpreter
uses a state that is modified for each command evaluation. At each
step, we need to remember the whole program, the next line to
interpret and the values of the variables. The program being
interpreted is not exactly the one that was entered in the toplevel:
instead of a list of commands, it is an array of commands. Thus
the state of a program during execution is:
# type state_exec = { line:int ; xprog:code ; xenv:environment } ;;
Two different reasons may lead to an error during the evaluation of a
line: an error while computing an expression, or branching to an
absent line. They must be dealt with so that the interpreter exits
nicely, printing an error message. We define an exception as well as a
function to raise it, indicating the line where the error occurred.
# exception RunError of int
let runerr n = raise (RunError n) ;;
exception RunError of int
val runerr : int -> 'a = <fun>
Assembly
Assembling a program that is a list of numbered lines (type
program) consists of transforming this list into an array and
modifying the flow control commands. This last modification only
needs an association table between line numbers and array indexes.
This is easily provided by storing lines (with their line numbers),
instead of commands, in the array: to find the association between
a line number and the index in the array, we look the line number up
in the array and return the corresponding index. If no line is found
with this number, the index returned is -1.
# exception Result_lookup_index of int ;;
exception Result_lookup_index of int
# let lookup_index tprog num_line =
try
for i=0 to (Array.length tprog)-1 do
let num_i = tprog.(i).num
in if num_i=num_line then raise (Result_lookup_index i)
else if num_i>num_line then raise (Result_lookup_index (-1))
done ;
(-1 )
with Result_lookup_index i -> i ;;
val lookup_index : line array -> int -> int = <fun>
# let assemble prog =
let tprog = Array.of_list prog in
for i=0 to (Array.length tprog)-1 do
match tprog.(i).cmd with
Goto n -> let index = lookup_index tprog n
in tprog.(i) <- { tprog.(i) with cmd = Goto index }
| If(c,n) -> let index = lookup_index tprog n
in tprog.(i) <- { tprog.(i) with cmd = If (c,index) }
| _ -> ()
done ;
tprog ;;
val assemble : line list -> line array = <fun>
Expression evaluation
The evaluation function does a depth-first traversal on the abstract syntax
tree, and executes the operations indicated at each node.
The RunError exception is raised in case of type
inconsistency, division by zero, or an undeclared variable.
# let rec eval_exp n envt expr = match expr with
ExpInt p -> Vint p
| ExpVar v -> ( try List.assoc v envt with Not_found -> runerr n )
| ExpUnr (UMINUS,e) ->
( match eval_exp n envt e with
Vint p -> Vint (-p)
| _ -> runerr n )
| ExpUnr (NOT,e) ->
( match eval_exp n envt e with
Vbool p -> Vbool (not p)
| _ -> runerr n )
| ExpStr s -> Vstr s
| ExpBin (e1,op,e2)
-> match eval_exp n envt e1 , op , eval_exp n envt e2 with
Vint v1 , PLUS , Vint v2 -> Vint (v1 + v2)
| Vint v1 , MINUS , Vint v2 -> Vint (v1 - v2)
| Vint v1 , MULT , Vint v2 -> Vint (v1 * v2)
| Vint v1 , DIV , Vint v2 when v2<>0 -> Vint (v1 / v2)
| Vint v1 , MOD , Vint v2 when v2<>0 -> Vint (v1 mod v2)
| Vint v1 , EQUAL , Vint v2 -> Vbool (v1 = v2)
| Vint v1 , DIFF , Vint v2 -> Vbool (v1 <> v2)
| Vint v1 , LESS , Vint v2 -> Vbool (v1 < v2)
| Vint v1 , GREAT , Vint v2 -> Vbool (v1 > v2)
| Vint v1 , LESSEQ , Vint v2 -> Vbool (v1 <= v2)
| Vint v1 , GREATEQ , Vint v2 -> Vbool (v1 >= v2)
| Vbool v1 , AND , Vbool v2 -> Vbool (v1 && v2)
| Vbool v1 , OR , Vbool v2 -> Vbool (v1 || v2)
| Vstr v1 , PLUS , Vstr v2 -> Vstr (v1 ^ v2)
| _ , _ , _ -> runerr n ;;
val eval_exp : int -> (string * value) list -> expression -> value = <fun>
Command evaluation
To evaluate a command, we need a few additional functions.
We add an association to an environment by removing a previous
association for the same variable name if there is one:
# let rec add v e env = match env with
[] -> [v,e]
| (w,f)::l -> if w=v then (v,e)::l else (w,f)::(add v e l) ;;
val add : 'a -> 'b -> ('a * 'b) list -> ('a * 'b) list = <fun>
A function that prints the value of an integer or string is useful
for evaluation of the PRINT command.
# let print_value v = match v with
Vint n -> print_int n
| Vbool true -> print_string "true"
| Vbool false -> print_string "false"
| Vstr s -> print_string s ;;
val print_value : value -> unit = <fun>
The execution of a command corresponds to a transition from one
state to another. More precisely, the environment is modified if the
command is an assignment. Furthermore, the next line to execute is always
modified. As a convention, if the next line to execute does not exist,
we set its value to -1
# let next_line state =
let n = state.line+1 in
if n < Array.length state.xprog then n else -1 ;;
val next_line : state_exec -> int = <fun>
# let eval_cmd state =
match state.xprog.(state.line).cmd with
Rem _ -> { state with line = next_line state }
| Print e -> print_value (eval_exp state.line state.xenv e) ;
print_newline () ;
{ state with line = next_line state }
| Let(v,e) -> let ev = eval_exp state.line state.xenv e
in { state with line = next_line state ;
xenv = add v ev state.xenv }
| Goto n -> { state with line = n }
| Input v -> let x = try read_int ()
with Failure "int_of_string" -> 0
in { state with line = next_line state;
xenv = add v (Vint x) state.xenv }
| If (t,n) -> match eval_exp state.line state.xenv t with
Vbool true -> { state with line = n }
| Vbool false -> { state with line = next_line state }
| _ -> runerr state.line ;;
val eval_cmd : state_exec -> state_exec = <fun>
On each call of the transition function eval_cmd, we
look up the current line, run it, then set the number of the next
line to run as the current line. If the last line of the program is
reached, the current line is given the value -1. This
will tell us when to stop.
Program evaluation
We recursively apply the transition function until we reach a state
where the current line number is -1.
# let rec run state =
if state.line = -1 then state else run (eval_cmd state) ;;
val run : state_exec -> state_exec = <fun>
Finishing touches
The only thing left to do is to write a small editor and to plug
together all the functions we wrote in the previous sections.
The insert function adds a new line in the program at the
requested place.
# let rec insert line p = match p with
[] -> [line]
| l::prog ->
if l.num < line.num then l::(insert line prog)
else if l.num=line.num then line::prog
else line::l::prog ;;
val insert : line -> line list -> line list = <fun>
The print_prog function prints the source code of a
program.
# let print_prog prog =
let print_line x = print_string (pp_line x) ; print_newline () in
print_newline () ;
List.iter print_line prog ;
print_newline () ;;
val print_prog : line list -> unit = <fun>
The one_command function processes the insertion of a line
or the execution of a command. It modifies the state of the toplevel
loop, which consists of a program and an environment. This
state, represented by the loop_state type, is different from
the evaluation state.
# type loop_state = { prog:program; env:environment } ;;
# exception End ;;
# let one_command state =
print_string "> " ; flush stdout ;
try
match parse (input_line stdin) with
Line l -> { state with prog = insert l state.prog }
| List -> (print_prog state.prog ; state )
| Run
-> let tprog = assemble state.prog in
let xstate = run { line = 0; xprog = tprog; xenv = state.env } in
{state with env = xstate.xenv }
| PEnd -> raise End
with
LexerError -> print_string "Illegal character\n"; state
| ParseError -> print_string "syntax error\n"; state
| RunError n ->
print_string "runtime error at line ";
print_int n ;
print_string "\n";
state ;;
val one_command : loop_state -> loop_state = <fun>
The main function is the go function, which starts the
toplevel loop of our Basic.
# let go () =
try
print_string "Mini-BASIC version 0.1\n\n";
let rec loop state = loop (one_command state) in
loop { prog = []; env = [] }
with End -> print_string "See you later...\n";;
val go : unit -> unit = <fun>
The loop is implemented by the local function loop. It
stops when the End exception is raised by the
one_command function.
Example: C+/C-
We return to the example of the C+/C- game described in chapter 3,
page ??. Here is the Basic program corresponding to that
Objective CAML program:
10 PRINT "Give the hidden number: "
20 INPUT N
30 PRINT "Give a number: "
40 INPUT R
50 IF R = N THEN 110
60 IF R < N THEN 90
70 PRINT "C-"
80 GOTO 30
90 PRINT "C+"
100 GOTO 30
110 PRINT "CONGRATULATIONS"
And here is a sample run of this program.
> RUN
Give the hidden number:
64
Give a number:
88
C-
Give a number:
44
C+
Give a number:
64
CONGRATULATIONS
Further work
The Basic we implemented is minimalist. If you want to go further,
the following exercises hint at some possible extensions.
- Floating-point numbers: as is, our language only deals with
integers, strings and booleans. Add floats, as well as the
corresponding arithmetic operations in the language grammar. We need
to modify not only parsing, but also evaluation, taking into
account the implicit conversions between integers and floats.
- Arrays: Add to the syntax the command DIM
var[x] that declares an array var of size x, and the
expression var[i] that references the ith element of the
array var.
- Toplevel directives: Add the toplevel directives SAVE "file_name" and LOAD "file_name" that save a Basic
program to the hard disk, and load a Basic program from the hard
disk, respectively.
- Sub-program: Add sub-programs. The GOSUB line
number command calls a sub-program by branching to the given
line number while storing the line from where the call is made. The
RETURN command resumes execution at the line following the
last GOSUB call executed, if there is one, or exits the
program otherwise. Adding sub-programs requires evaluation to
manage not only the environement but also a stack containing the
return addresses of the current GOSUB calls. The GOSUB
command adds the possibility of defining recursive sub-programs.