From Eq. (6.5), we have
![]() , so that the
frequency response is
, so that the
frequency response is
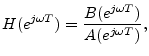
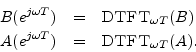
As before,
denotes the (bilateral) discrete time Fourier transform (DTFT).From the above relations, we may express the frequency response of any IIR filter as a ratio of two finite DTFTs: