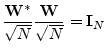With the above definition for paraconjugation of a MIMO transfer-function
matrix, we may generalize the MIMO allpass condition Eq. (D.2) to the
entire ![]() plane as follows:
plane as follows:
Theorem:
Every lossless ![]() transfer function matrix
transfer function matrix
![]() is paraunitary,
i.e.,
is paraunitary,
i.e.,
By construction, every paraunitary matrix transfer function is
unitary on the unit circle for all ![]() . Away from the
unit circle, the paraconjugate
. Away from the
unit circle, the paraconjugate
![]() is the unique analytic
continuation of
is the unique analytic
continuation of
![]() (the Hermitian transpose of
(the Hermitian transpose of
![]() ).
).
Example:
The normalized DFT matrix is an ![]() order zero
paraunitary transformation. This is because the normalized DFT
matrix,
order zero
paraunitary transformation. This is because the normalized DFT
matrix,
![]() , where
, where
![]() , is a
unitary matrix:
, is a
unitary matrix: