Multi-Input, Multi-Output (MIMO)
Allpass Filters

To generalize lossless filters to the multi-input, multi-output (MIMO) case, we must generalize conjugation to MIMO transfer function matrices:

Theorem: A $p\times q$ transfer function matrix $\mathbf{H}(z)$ is lossless if and only if its frequency-response matrix $\mathbf{H}(e^{j\omega})$ is unitary, i.e.,

$$\mathbf{H}^*(e^{j\omega})\mathbf{H}(e^{j\omega}) = \mathbf{I}_q \protect$$ (D.2)

for all $\omega$, where $\mathbf{I}_q$ denotes the $q\times q$ identity matrix, and $\mathbf{H}^\ast(e^{j\omega})$ denotes the Hermitian transpose (complex-conjugate transpose) of $\mathbf{H}(e^{j\omega})$:

$$\mathbf{H}^*(e^{j\omega}) \isdef \overline{\mathbf{H}^T(e^{j\omega})}$$

Let $\underline{y}_p(n)$ denote the length $p$ output vector at time $n$, and let ${\underline{x}}_q(n)$ denote the input $q$-vector at time $n$. Then in the frequency domain we have $\underline{Y}_p(e^{j\omega})=\mathbf{H}(e^{j\omega})\underline{X}_q(e^{j\omega})$, which implies

$$\underline{Y}_p^*\underline{Y}_p = \underline{X}_q^*\underbrace{\... ...H}(e^{j\omega})}_{\mathbf{I}_q}\underline{X}_q = \underline{X}^*\underline{X},$$

or

$$\sum_{i=1}^p\left\vert Y_i(e^{j\omega})\right\vert^2 = \sum_{i=1}^q\left\vert X_i(e^{j\omega})\right\vert^2.$$

Integrating both sides of this equation with respect to $\omega$ yields that the total energy in equals the total energy out, as required by the definition of losslessness.

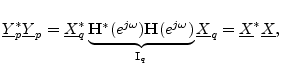
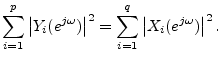
We have thus shown that in the MIMO case, losslessness is equivalent to having a unitary frequency-response matrix. A MIMO allpass filter is therefore any filter with a unitary frequency-response matrix.

Note that $\mathbf{H}^*(e^{j\omega})\mathbf{H}(e^{j\omega})$ is a $q\times q$ matrix product of a $q\times p$ times a $p\times q$ matrix. If $q>p$, then the rank must be deficient. Therefore, $p\geq q$. (There must be at least as many outputs as there are inputs, but it's ok to have extra outputs.)