Minimum-Phase/Allpass Decomposition

Every causal stable filter $H(z)$ with no zeros on the unit circle can be factored into a minimum-phase filter in cascade with a causal stable allpass filter:

$$H(z) = H_{\hbox{mp}}(z)S(z) \qquad\hbox{(Minimum-Phase/Allpass Decomposition)}$$

where $H_{\hbox{mp}}(z)$ is minimum phase, $S(z)$ is an allpass filter

$$S(z) = \frac{s_L + s_{L-1}z^{-1}+ \cdots + s_1 z^{-(L-1)} + z^{-L}} {1 + s_1z^{-1}+ s_2 z^{-2}+ \cdots + s_L z^{-L}},$$

and $L$ is the number of non-minimum-phase zeros of $H(z)$.

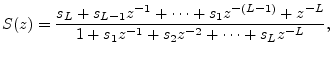
This result is easy to show by induction. Consider a single non-minimum-phase zero $\xi$ of $H(z)$. Then $\left\vert\xi\right\vert>1$, and $H(z)$ can be written with the non-minimum-phase zero factored out as

$$H(z) = H_1(z) (1-\xi z^{-1}).$$

Now multiply by $1=(1-\xi^{-1}z^{-1})/(1-\xi^{-1}z^{-1})$ to get

$$H(z) = \underbrace{H_1(z) (1-\xi^{-1}z^{-1})}_{\displaystyle\isde... ...underbrace{\frac{1-\xi z^{-1}}{1-\xi^{-1}z^{-1}}}_{\displaystyle\isdef S_1(z)}$$

We have thus factored $H(z)$ into the product of $H_2(z)$, in which the non-minimum-phase zero has been reflected inside the unit circle to become minimum-phase (from $z=\xi$ to $z=1/\xi$), times a stable allpass filter $S_1(z)$ consisting of the original non-minimum-phase zero $\xi$ and a new pole at $z=1/\xi$ (which cancels the reflected zero at $z=1/\xi$ given to $H_2(z)$). This procedure can now be repeated for each non-minimum-phase zero in $H(z)$.

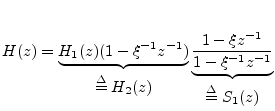
In summary, we may factor non-minimum-phase zeros out of the transfer function and replace them with their minimum-phase counterparts (not altering the amplitude response).

A procedure for computing the minimum phase for a given spectral magnitude is given in §12.4. More theory pertaining to minimum phase sequences may be found in [60].