The Discrete Cosine Transform (DCT)

In image coding (such as MPEG and JPEG), and many audio coding algorithms (MPEG), the discrete cosine transform (DCT) is used because of its nearly optimal asymptotic theoretical coding gain.^A.12For 1D signals, one of several DCT definitions (the one called DCT-II)^A.13is given by

$$\hbox{\sc DCT}_k(x) = 2\sum_{n=0}^{N-1} x(n) \cos\left[\frac{\pi k}{2N}(2n+1)\right], \quad k=0,1,2,\ldots,N-1$$

$$= 2\sum_{n=0}^{N-1} x(n) \cos\left[\omega_k\left(n+\frac{1}{2}\right)\right] \protect$$ (A.2)

where

$$\omega_k \isdef \frac{2\pi}{2N}k.$$

Note that $\omega_k$ is the DFT frequency for a length $2N$ DFT (as opposed to $N$).

For real signals, the real part of the DFT is a kind of DCT:

$$\begin{eqnarray*} \mbox{re}\left\{\hbox{\sc DFT}_k(x)\right\} &\isdef & \mbox{r... ...right\}\\ &=& \sum_{n=0}^{N-1} x(n) \cos\left(\omega_k n\right) \end{eqnarray*}$$

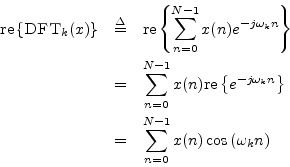
Thus, the real part of a double-length FFT is the same as the DCT except for the half-sample phase shift in the sinusoidal basis functions $s_k(n) = e^{j\omega_k n}$ (and a scaling by 2 which is unimportant).

In practice, the DCT is normally implemented using the same basic efficiency techniques as in FFT algorithms. In Matlab, the functions dct and dct2 are available for the 1D and 2D cases, respectively.

Exercise: Using Euler's identity, expand the cosine in the DCT defined by Eq. (A.2) above into a sum of complex sinusoids, and show that the DCT can be rewritten as the sum of two phase-modulated DFTs:

$$\hbox{\sc DCT}_{N,k} = e^{j\omega_k\frac{1}{2}} \overline{X_{2N}(\omega_k)} +e^{-j\omega_k\frac{1}{2}} X_{2N}(\omega_k)$$

where $X_{2N}(\omega_k)=\hbox{\sc DFT}_{2N,k}(x)$ denotes the length $2N$ DFT of $x$.