Theorem: For all
Theorem: For all
![]() ,
,
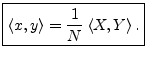
Proof:
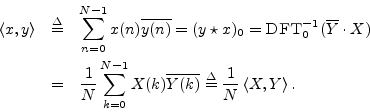
Note that the power theorem would be more elegant
if the DFT were defined as the coefficient of
projection onto the normalized DFT sinusoid
![]() . That, for the normalized DFT (defined in
§6.10), the power theorem becomes simply
. That, for the normalized DFT (defined in
§6.10), the power theorem becomes simply
The power theorem is also sometimes called Parseval's theorem [51].
In the field of physics, much progress has been made by formulating
physical laws such that they are invariant with respect to
changes of coordinates. The inner product is an example of a
coordinate-invariant relationship between two vectors ![]() and
and ![]() in
in
![]() . In the present setting, as developed in Chapter 5, we are
concerned only with two different coordinate systems,
corresponding to time-domain signals and their spectra.
. In the present setting, as developed in Chapter 5, we are
concerned only with two different coordinate systems,
corresponding to time-domain signals and their spectra.