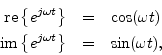
Interpreting the real and imaginary parts of the complex sinusoid,
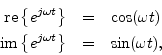
in the complex plane, we see that sinusoidal motion is the
projection of circular motion onto any straight line. Thus, the
sinusoidal motion
![]() is the projection of the circular
motion
is the projection of the circular
motion
![]() onto the
onto the ![]() (real-part) axis, while
(real-part) axis, while
![]() is the projection of
is the projection of
![]() onto the
onto the ![]() (imaginary-part) axis.
(imaginary-part) axis.
Figure 4.9 shows a plot of a complex sinusoid versus time, along with its
projections onto coordinate planes. This is a 3D plot showing the
![]() -plane versus time. The axes are the real part, imaginary part, and
time. (Or we could have used magnitude and phase versus time.)
-plane versus time. The axes are the real part, imaginary part, and
time. (Or we could have used magnitude and phase versus time.)
Note that the left projection (onto the ![]() plane) is a circle, the lower
projection (real-part vs. time) is a cosine, and the upper projection
(imaginary-part vs. time) is a sine. A point traversing the plot projects
to uniform circular motion in the
plane) is a circle, the lower
projection (real-part vs. time) is a cosine, and the upper projection
(imaginary-part vs. time) is a sine. A point traversing the plot projects
to uniform circular motion in the ![]() plane, and sinusoidal motion on the
two other planes.
plane, and sinusoidal motion on the
two other planes.