Miss In The Middle Attack on reduced variants the Block Cipher IDEA

· addition of integers modulo 2^16 where the 16bit subblock is treated as
the usual radixtwo representation of an integer, the resulting operation
is denoted as .

· multiplication of integers modulo 2^16+1 where the 16bit subblock is
treated as the usual radixtwo representation of an integer except that
the allzero subblock is treated as representing 2^16, the resulting
operation is denoted as .

As an example of these group operations, note that (remember that 0=2^16)

(0,...,0)(1,0,...,0) = (0,1,...,1,0) because 2^16*2^15 mod (2^16+1) =

2^15+1.

The 64bit plaintext block X is partitioned into four 16bit subblocks X1, X2,

X3, X4 i.e., X = (X1, X2, X3, X4). The four plaintext subblocks are then

transformed into four 16bit ciphertext subblocks Y1, Y2, Y3, Y4 [i.e., the

ciphertext block is Y = (Y1, Y2, Y3, Y4)] under the control of 52 key subblocks

of 16 bits that are formed from the 128bit secret key in a manner to be

described below. For r = 1,2,...,8, the six key subblocks used in the rth round

will be denoted as . Four 16-bit key subblocks are used in the

output transformation; these subblocks will be denoted as .

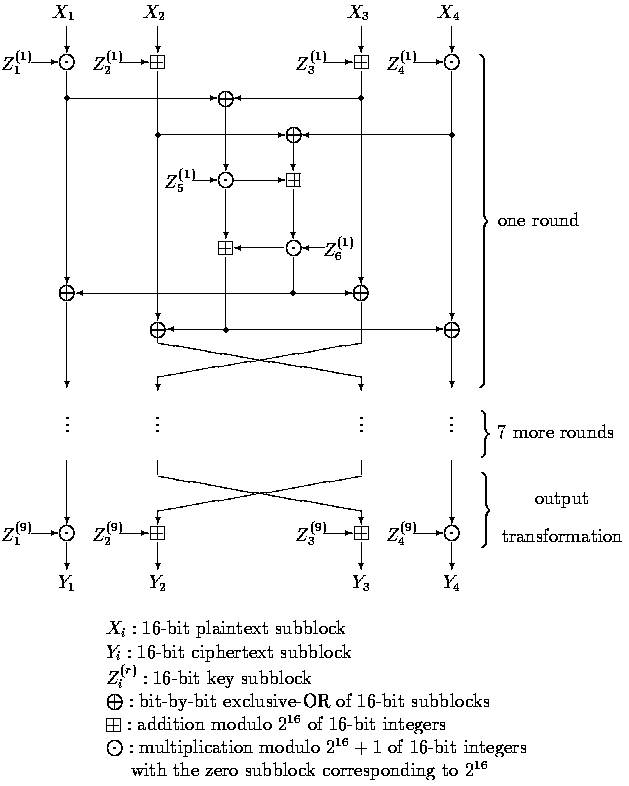
Figure 3.1: Computational graph for the encryption process of the IDEA cipher.

The decryption process

The computational graph of the decryption process is essentially the same

as that of the encryption process, the only change being that the decryption key

subblocks are computed from the encryption key subblocks as follows:

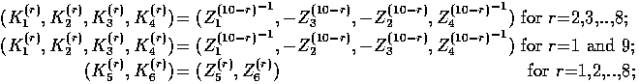
where Z^(-1) denotes the multiplicative inverse (modulo 2^16+1) of Z, i.e.,

ZZ^(-1)=1 and -Z denotes the additive inverse (modulo 2^16) of Z, i.e.,

-ZZ=0.

The computation of decryption key subblocks from the encryption key subblocks is

also shown in Table.1.

The Key schedule

The 52 key subblocks of 16 bits used in the encryption process are

generated from the 128bit userselected key as follows: The 128bit

userselected key is partitioned into 8 subblocks that are directly used as the

first eight key subblocks, where the ordering of the key subblocks is defined as

follows: . The

128bit userselected key is then cyclic shifted to the left by 25 positions,

after which the resulting 128bit block is again partitioned into eight

subblocks that are taken as the next eight key subblocks. The obtained 128bit

block is again cyclic shifted to the left by 25 positions to produce the next

eight key subblocks, and this procedure is repeated until all 52 key subblocks

have been generated.

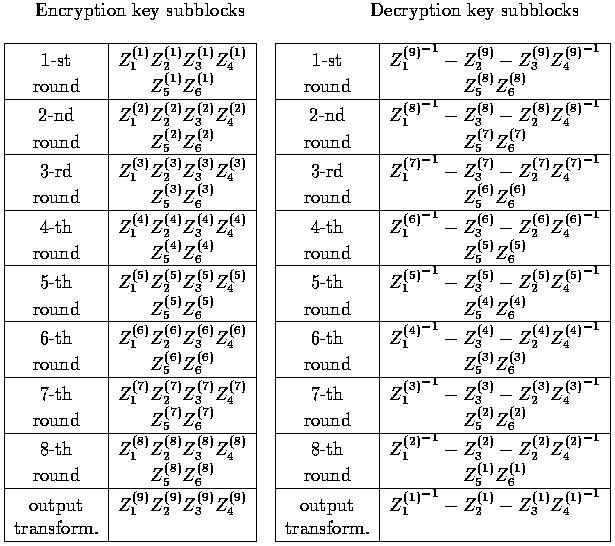
Table.1: The encryption and decryption key subblocks

________________________________________________________________________________

Part II: The description of the Miss In The Middle attack

on IDEA reduced to 3.5 rounds (by E. Biham, A. Biryukov

and A. Shamir)

Introduction

The general idea of Miss In The Middle attack is to construct an

impossible differential for some portion of consecutive rounds of a given cipher

and then use it in order to disqualify as many possibilities for some subset of

key bits as possible. The way it is done in the Miss In The Middle attack on

IDEA is as follows:

· Two half rounds are added to the "impossible differential rounds" (i.e.
the consecutive rounds that exhibit the impossible differential).

· Structures containing plain text/cipher text pairs are created following
restrictions that will allow an impossible differential to occure for some
possibilities of some subset of key bits.

· All the possibilities of several subkeys of the added two "outer" half
rounds that exhibit the impossible differential for the "inner" rounds for
some pair in some structure are eliminated.

· The elimination process continues until we have only few possibilities
left for the subset of the key bits on which we eliminate.

The rest of the key bits (the ones that are not found by using any impossible

differential for the "inner" rounds) are found by an exhaustive search.

The following sections will introduce some notations which will later be used in

a detail description of the attack on IDEA reduced to 3.5 rounds (using two 2.5

round impossible differentials). The first 3 sections are taken from the

article: "Miss in the Middle Attacks on IDEA, Khufu and Khafre" by E. Biham, A.

Biryukov and A. Shamir, they describe an attack on rounds 1-4 (rounds are

numbered: 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, ... and thus rounds 1-4 is 3.5 round

IDEA) of the full variant of IDEA. Following them is part III containing a

detail description of my implementation of the attack on the reduced variant of

IDEA - 32 bit blocks with 64 bit key (using the same key schedule of the

original cipher). The implementation attacks rounds 1-4 of the reduced cipher.

Notations

IDEA is an 8.5 round cipher using two different halfround operations:

key mixing (which we denote by T ) and Mmixing denoted by , where

MA denotes a multiplicationaddition structure and s denotes a swap of two

middle words. Both MA and s are involutions. T divides the 64bit block into

four 16bit words and mixes the key to the data using multiplication modulo

2^16 + 1 (denoted by ) with 0=2^16 on words one and four, and using addition

modulo 2^16 (denoted by ) on words two and three. The full 8.5-round IDEA can

be written as:

Input to the key mixing step T in round i is denoted by Xi (in our notation Xi

Denotes ), and its output (the input to M) by Yi . The rounds are numbered

from one and the plaintext is thus denoted by X1. See Picture 2 for a picture of

one round of IDEA.

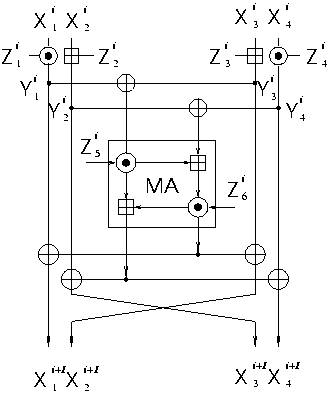
Picture.2 One round of IDEA in new notations.

Additional notation: will be denoted by X(i,j) (the same goes for Y),

difference in X(i,j) will be denoted by X'(i,j).

A 2.5round Impossible Differential of IDEA

The main observation is that IDEA has a 2.5-round differential with

probability zero.

Consider the 2.5 rounds . Then the input difference (a,0,a,0)

(where 0 and a<>0 are 16bit words) cannot cause the output difference (b,b,0,0)

after 2.5 rounds for any b<>0. To prove this claim, make the following

observations:

1. Consider a pair with an input difference (a,0,a,0) for a<>0. In such a
pair, the inputs to the first MAstructure have difference zero, and the
outputs of the first MA have difference zero. Thus, the difference after
the first halfround is (a,a,0,0) (after the swap of the two
middle words). After the next halfround (T) the difference becomes
(c,d,0,0) for some c<>0 and d<>0.

2. Similarly, consider a pair with an output difference (b,b,0,0) for b<>0
after 2.5 rounds. In such a pair the difference before the last halfround
(M) is (b,0,b,0), and the difference before the last T is of the form
(e,0,f,0) for some e<>0 and f<>0.

3. Therefore, if the input and output differences are both as above, the
input difference of the middle halfround (M) is (c,d,0,0), and the output
difference of the same halfround is (e,0,f,0). The difference before the
swap of the two middle words is (e,f,0,0). From these differences we
conclude that the differences of the inputs to the MAstructure in the
middle halfround is nonzero (c,d)=(e,f), while the output difference is
)ce,df) =(0,0). This is a contradiction, as the MAstructure is a
permutation. Consequently, there are no pairs satisfying both the input
and the output differences simultaneously.

Due to symmetry there is another impossible 2.5round differential, with input

difference (0,a,0,a) and output difference (0,0,b,b).

An Attack on 3.5Round IDEA

Consider the first 3.5 rounds of IDEA . We denote the plaintext

by X1 and the ciphertext by Y4 . The attack is based on the 2.5round impossible

differential with two additional T halfrounds at the beginning and end, and

consists of the following steps:

1. Choose a structure of 2^32 plaintexts X1 with identical X(1,2) , identical
X(1,4), and all possibilities of X(1,1) and X(1,3).

2. Collect about 2^31 pairs from the structure whose ciphertexts satisfy
Y'(4,3)=0 and Y'(4,4)=0.

3. For each such pair:

a. Try all the 2^32 possible subkeys of the first T halfround that
affect X(1,1) and X(1,3), and partially encrypt X(1,1) and X(1,3)
into Y(1,1) and Y(1,3) in each of the two plaintexts of the pair.
Collect about 2^16 possible 32bit subkeys satisfying Y'(1,1) =
Y'(1,3). This step can be done efficiently with 2^16 time and memory
complexity.

b. Try all the 2^32 possible subkeys of the last T halfround that
affect X(4,1) and X(4,2), and partially decrypt Y(4,1) and Y(4,2)
into X(4,1) and X(4,2) in each of the two ciphertexts of the pair.
Collect about 2^16 possible 32bit subkeys satisfying X'(4,1) =
X'(4,2). This step can be done efficiently with 2^16 time and memory
complexity.

c. Make a list of all the 2^32 64bit subkeys combining the previous
two steps. These subkeys cannot be the real value of the key, as if
they do, there is a pair satisfying the differences of the
impossible differential.

4. Repeat this analysis for each one of the 2^31 pairs obtained in each
structure and use a total of about 90 structures. Each pair defines a list
of about 2^32 incorrect keys. Compute the union of the lists of impossible
64bit subkeys they suggest. It is expected that after about 90
structures, the number of remaining wrong key values is:
and thus the correct key can be
identified as the only remaining value.

5. Complete the secret key by analyzing the second differential:
(0,a,0,a)-x->(0,0,b,b). Similar analysis will give 46 new key bits (16
bits out of 64 are in common with the bits that we already found, and two
bits 17 and 18 are common between the 1st and 4th rounds of this
differential). Finally guess the 18 bits that are still not found to
complete the 128-bit secret key.

This attack requires about 2^38.5 chosen plaintexts and about 2^53 steps of

Analysis. This analysis requires only about 2^48 memory (apart from the memory

required to keep the plaintexts and the ciphertexts) when performed in a

slightly different order.

________________________________________________________________________________

Part III: Implementation of the the described Miss In The

Middle (MIM) technique for a MIM attack on reduced

(32-bit block) variant of IDEA reduced to it's first 3.5

rounds

Introduction

Here we'll implement the MIM technique presented above. In the first

section of this part we'll list some small adjustments to the above MIM attack

(on full variant of IDEA reduced to 3.5 rounds) description presented in secton:

"An Attack on 3.5Round IDEA" of part II. The adjustments are concerned only

with the numbers in the above description, since the attack is exactly the same

but the numbers change due to the reduction of the cipher to 32 bit blocks.

In the second section there is a detail description of the implimentation

itself, listing all the key functions and structures.

Third section concludes the results.

List of adjustments to the part II MIM attack description

First let's present key schedule (list of subkeys) for the reduced variant

of IDEA (from here on, when I write reduced variant of the IDEA, it denotes the

first 3.5 rounds of 32 bit block, 64-bit key IDEA):

Round/Subkey	1	2	3	4	5	6
1	[1..8]	[9..16]	[17..24]	[25..32]	[33..40]	[41..48]
2	[49..56]	[57..64]	[26..33]	[34..41]	[42..49]	[50..57]
3	[58..1]	[2..9]	[10..17]	[18..25]	[51..58]	[59..2]
4	[3..10]	[11..18]	[19..26]	[27..34]	X	X

in the above table [x..y] signifies some subkey of the reduced variant, i.e. it

is a range of 8 key bits that form that subkey (in our notations the leftmost

key of the 64 bit key is key bit #1 and rightmost key bit is key bit #64, this

notation is also used in the program).

As you'll see in the detailed description the implementation of the attack

consists of two main parts (the third one is an exhaustive search): first one

uses the first impossible differential (A,0,A,0)-x->(B,B,0,0) and as clearely

seen from the above table, it gives us the bits:

[1..8]U[17..24]U[3..10]U[11..18]=[1..24] of the key. The second part of the

attack uses impossible differential (0,A,0,A)-x->(0,0,B,B) (and the knowledge of

the already discovered key bits [1..24]), thus giving us knwoledge of key bits:

[9..16]U[25..32]U[19..26]U[27..34]=[9..16]U[19..34], which together with bits

[1..24] we'll have key bits [1..34] after running the second part (the rest of

the key bits: [35..64] are "exhaustively" searched for).

Here is the list of adjustments for the section "An Attack on 3.5Round IDEA" of

part II, that are nessecary for it to become the description of the general

attack algorithm used in the implementation (here we use the same numbering

notation as in the intended section, changes are described only where they're

needed):

1. Obviously our strucure will contain 2^16 plaintexts (the structures are
constructed due to the same restrictions).

2. Also obviouse that we expect to collect 2^15 pairs with Y'(4,3)=Y'(4,4)=0
since we have (2^16*2^16)/2=2^31 distinct plaintext pairs and a chance of
Y'(4,3)=Y'(4,4)=0 for some plaintext pair is obviously 1/(2^8*2^8)=2^(-16)
and thus E[plaintext pairs with Y'(4,3)=Y'(4,4)=0] = 2^31*2^(-16)=2^15
(expectation of binomial distribution).

3. The adjustments to the elimination process:

a. In our case we have only 2^16 possible subkeys that affect X(1,1)
and X(1,3). In our case we expect to get about 2^8 possible 16-bit
subkeys that satisfy Y'(1,1)=Y'(1,3) (for each of the 2^8
possibilities for Z(1,3) there is at least one option for Z(1,1)
that satisfies the above equasion). This step is done in 2^8 time
and memory complexity.

b. The same adjustments as in (a).

c. In our case (as it was previously shown), we are working with only
24-bit subkeys, moreover for the pair of subkeys found in (a) and
(b) be "compatable" (i.e. form a "legitemit" impossible 24-bit
subkey) they should have the same value for their shared bits:
[3..8]U[17..18]. So since from (a) and (b) we get 2^16 candidates
for impossible 24-bit subkeys and a chance for the candidate to be
"ligit." is 2^(-8) (obviouse as there are 8 shared bits), then in
step (c) we expect to have a list of 2^16*2^(-8)=2^8 impossible
24-bit keys.

4. In our case we need 36 structures, since after eliminating on those 36
structures we expect to have 2^24*[1-2^(-16)]^(2^15*36) = 0.26 < 1
possibilities left for bits [1..24] of the key.

5. For the case of the second impossible differential (the search for
additional 10 key bits [25..34]): we already know 14 bits of the subkey
involved, so in (3)(a) only one subkey is expected, in (3)(b) 4 subkeys
and since (3)(a)'s and (3)(b)'s subkeys still share 8 bits, then the
probability for a "legit." impossible 10-bit subkey remains 2^(-8) and
thus we need 64 (3)'s pairs to get one "legit." impossible 10-bit subkey.
So we conclude that we need 16 structures so that the # of remainig keys
will be 2^10*[1-2^(-16)]^(2^15*16) = 0.34 < 1.

(P.S.: theory is good but it sometimes disagrees with reality, test results show

that in fact we need about 32 structures in (5), i.e. twice the expected number,

but this may also be from the lack of true randomness of the rand() function).

Detail description of the attack's implementation

Remark: For the sake of code readability I've partitioned the program into 3

parts:

1. Part A: it makes use of impossible differential A0A0-x->BB00 in order to
find bits [1..24] of the key.

2. Part B: there we find bits [25..34] of the key, while using the knoledge
obtained in part A.

3. Part C: it is an exhaustive search for the remainder of the key bits (bits
[35..64]).

For clearity in the code I've implemented part A and part B in a separate
namespaces: PartA and PartB accordingly.

A Complete List of Global Functions (GF), Global Structures (GS) and Global Variables (GV)

1. LIST (GS) - defined as "std::vector<unsigned>" (i.e. instance of standard
library vector template as vector of unsigned integers).

2. KEY (GV) - declared as "unsigned int KEY[6][9]" is used as an array of
subkeys for encryption, where KEY[i][j] is subkey j of round i (0<j<5,
0<i<8).

3. mul (GF) - declared as "unsigned int mul(unsigned int a, unsigned int b)",
it performs multiplication of to 8-bit integers modulu 2^8+1.

4. cip (GF) - declared as "void cip(unsigned int XX[4], unsigned int YY[4],
unsigned int Z[6][9])", it is the encipherer (taken from the Lai and
Massey book) for rounds 1 – 4 (without half round 4.5). It gets the input
4 bytes: the lower bytes of XX[4] and it produces the output 4 bytes: the
lower bytes of YY[4].
(Remark: by lower bytes I mean LOGICAL lower bytes, i.e X&0xff (int = 4 bytes)).

5. key (GF) - declared as "void key(unsigned int uskey[2])", this function is
the IDEA subkey generator. IDEA key schedule is to partition the 64 bit
key into 8 subsiquent subkeys and then shift the key 25 places to the
left, then get the next subsequent subkeys the same way.

6. inv (GF) - declared as "unsigned int inv(unsigned int x)", auxilary
function that calculates an inverse of 8-bit integer x modulu 2^8+1 using
the GCD algorithm.

7. Pair (GS) - declared as "struct Pair", intended to hold the inp./outp.
value (used as elements of a structure).

Part A Functions (PAF) and Part A Variables (PAV)

1. Variants (PAV) - declared as "int *Variants", and is initialized to NULL. It will point to a block of 2^24 bits each bit signifing one
possibility for the first 24 bits of the real key.

2. NumKeysLeft (PAV) - declared as "unsigned int NumKeysLeft", and is
initialized to 0x1000000 (=2^24). During the elimination process it will
contain the number of 24-bit subkeys still remaining.

3. inv_arr (PAV) - declared as "unsigned int inv_arr[256]", auxillary array
that will be used for "fast" inverse computation, will be initialized to
array of inverses s.t.: [(inv_arr[i]*i) mod (2^8+1)] = 1

4. SDB (PAV) - declared as "Pair SDB[0x10000]", Sample Data Base, 2^16
entries, it will be used to contain structures of 2^16 plaintexts each.

5. Init (PAF) - declared as "void Init()", initialization function:
initializes the NumKeysLeft to 2^24, inv_arr to the intended values and
Variants array to a block of 2^24 zero bits.

6. Exclude (PAF) - declared as "int Exclude(unsigned int ip_key)", exludes
the given improper subkey (24-bit) from the Variants array by setting it's
bit to 1.

7. QueryKey (PAF) - declared as "int QueryKey(unsigned int key)", checks if
the given subkey (24-bit) was not previosly excluded (intended for BUG
detection).

8. GetAllRemainingKeys (PAF) – declared as "unsigned int
*GetAllRemainingKeys()"
it builds and returns an array of all the keys not previosly excluded (the
ones whose bit in Variants array is 0).

9. BuildSDB (PAF) - declared as "void BuildSDB(unsigned int x2,unsigned int
x4)". This function receives x2=X and x4=Y and filles the Pairs array SDB
with a structure of all the possible inputs of the type *X*Y with their
according outputs after 3.5 rounds of IDEA. Note that the difference
between plaintexts of each two elements of the structure is *0*0 and thus
it is the required structure for the attack.

10. GetAllBadFKH (PAF) - declared as "LIST **GetAllBadFKH(unsigned int
x1_mul, unsigned int x2_mul, unsigned int x1_add, unsigned int x2_add)".
It gets all bad First Key Halves (FKH), i.e. all the relevant 1-st round
subkey bits which make a (A,0,A,0) input difference (to the round 1.5) for
a given pair of plaintexts. Expected Complexity: O(2^8). The way it works
is as follows:

· We build an array of lists, each list contains all the subkeys
Z(1,1) which make the same Y'(1,1) and each list is indexed by
the Y'(1,1).

· Then we go over all the possible values of Z(1,3) and for each
value of Z(1,3), we calculate the resulting Y'(1,3), then for
each element of the list indexed by Y'(1,3) in the array built in
the previouse step, we combine Z(1,3) with the element of the
list to produce a 16-bit part of the impossible 24-bit subkey, we
then add each produced "part" to our output structure.

· The output structure of this function is an array of lists, each
containing first parts and indexed by the common value of the
shared bits of subkeys (Z(1,1),Z(1,3)) and (Z(4,1),Z(4,2)).

11. GetAllBadLKH (PAF) - declared as "LIST **GetAllBadLKH(unsigned int
x1_mul, unsigned int x2_mul, unsigned int x1_add, unsigned int x2_add)".
It gets all bad Last Key Halves (LKH), i.e. all the relevant 4-th round
subkey bits which make a (B,B,0,0) output difference (of round 3.5) for a
given pair of ciphertexts. Expected Complexity: O(2^8). It works exactly
the same way as GetAllBadFKH with minor difference: there we've enciphered
one half-round and here we decipher a half round to get the results. The
output structure is an array of lists, each containing the last parts of
impossible 24-bit subkeys, indexed by the shared bits (as in the previouse
function).

12. ExcludeResBadKeys (PAF) - declared as "void ExcludeResBadKeys(unsigned
int x11_mul, unsigned int x21_mul, unsigned int x11_add, unsigned int
x21_add, unsigned int x12_mul, unsigned int x22_mul, unsigned int x12_add,
unsigned int x22_add)". It excludes (from Variants structure) all the
improper (exhibiting the impossible 2.5 round differential for rounds
1.5-3.5 (including)) 24-bit subkeys for a given pair, expected O(2^16)
complexity. All it does is to run GetAllBadFKH and GetAllBadLKH, and then
combines the "parts" of an impossible 24-bit subkey that reside in lists
belonging to the same index (i.e. having common shared bits) in output
arrays of GetAllBadFKH and GetAllBadLKH, then it eliminates all the
resulting "legit." impossible keys from the Variants.

13. ExludeAllBadKeys (PAF) - declared as "void ExludeAllBadKeys(unsigned int
real_key)". It is the Attack itself! It takes the real 24 first bits of
the key for debugging reference (i.e. to see if we didn't made an error
and excluded the real key in some step). It excludes (if not previously
excluded) all the impossible 24-bit subkeys that we get from one
structure. First it finds all of the expected 2^15 pairs of structure
elements that exhibit (*,*,0,0) output difference in the 4-th half-round,
then on each resulting pair it runs ExcludeResBadKeys to exclude all of
the resulting impossible 24-bit subkeys. Expected complexity: O(2^31).

Part B Functions (PBF) and Part A Variables (PBV)

1. Variants (PBV) - declared as "int *Variants", and is initialized to
NULL. It will point to a block of 2^10 bits each bit signifing one
possibility for the bits 25..34 of the real key.

2. NumKeysLeft (PBV) - declared as "unsigned int NumKeysLeft", and is
initialized to 0x400 (=2^10). During the elimination process it will
contain the number of 10-bit subkeys still remaining.

3. inv_arr (PBV) - declared as "unsigned int inv_arr[256]", auxillary array
that will be used for "fast" inverse computation, will be initialized to
array of inverses s.t.: [(inv_arr[i]*i) mod (2^8+1)] = 1

4. SDB (PBV) - declared as "Pair SDB[0x10000]", Sample Data Base, 2^16
entries, it will be used to contain structures of 2^16 plaintexts each.

5. Init (PBF) - declared as "void Init()", initialization function:
initializes the NumKeysLeft to 2^10, inv_arr to the intended values and
Variants array to a block of 2^10 zero bits.

6. Exclude (PBF) - declared as "int Exclude(unsigned int ip_key)", exludes
the given improper subkey (10-bit) from the Variants array by setting it's
bit to 1.

7. QueryKey (PBF) - declared as "int QueryKey(unsigned int key)", checks if
the given subkey (10-bit) was not previosly excluded (intended for BUG
detection).

8. GetAllRemainingKeys (PAF) – declared as "unsigned int
*GetAllRemainingKeys()"
it builds and returns an array of all the keys not previosly excluded (the
ones whose bit in Variants array is 0).

9. BuildSDB (PBF) - declared as "void BuildSDB(unsigned int x1,unsigned int
x3)". This function receives x1=X and x3=Y and filles the Pairs array SDB
with a structure of all the possible inputs of the type X*Y* with their
according outputs after 3.5 rounds of IDEA. Note that the difference
between plaintexts of each two elements of the structure is 0*0* and thus
it is the required structure for the attack.

10. GetAllBadFKH (PBF) - declared as "LIST *GetAllBadFKH(unsigned int
x1_add, unsigned int x2_add, unsigned int x1_mul, unsigned int x2_mul,
unsigned int kb_9_to_16)". Exactly the same as it's twin PAF, with two
differences:

· It "works" for the second impossible differential: 0A0A-x->00BB.

· It gets already known (from part A) bits [9..16] (kb_9_to_16) of
the key and uses them.

11. GetAllBadLKH (PBF) - declared as "LIST **GetAllBadLKH(unsigned int
x1_add, unsigned int x2_add, unsigned int x1_mul, unsigned int x2_mul,
unsigned int kb_19_to_24)". Exactly the same as it's twin PAF, with two
differences:

· It "works" for the second impossible differential: 0A0A-x->00BB.

· It gets already known (from part A) bits [19..24] (kb_19_to_24)
of the key and uses them.

12. ExcludeResBadKeys (PBF) - declared as "void ExcludeResBadKeys(unsigned
int x11_add, unsigned int x21_add, unsigned int x11_mul, unsigned int
x21_mul, unsigned int x12_add, unsigned int x22_add, unsigned int x12_mul,
unsigned int x22_mul, unsigned int kb_9_to_16, unsigned int kb_19_to_24)".
Exactly the same as it's twin PAF, with three differences:

· It "works" for the second impossible differential: 0A0A-x->00BB.

· It gets already known (from part A) bits [9..16] (kb_9_to_16) of
the key and uses them.

· It gets already known (from part A) bits [19..24] (kb_19_to_24)
of the key and uses them.

13. ExludeAllBadKeys (PBF) - declared as "void ExludeAllBadKeys(unsigned int
kb_1_to_24)". Exactly the same as it's twin PAF, with two differences:

· It "works" for the second impossible differential: 0A0A-x->00BB.

· It gets already known (from part A) bits [1..24] (kb_1_to_24) of
the key and uses them.

Part C Functions (PCF)

* The following 2 functions are used for fast subkey generation in the
exhaustive search

1. key4elimInit (PCF) - declared as "void key4elimInit(unsigned int uk[2])".
It is an initialization function, takes all the known key bits (1 to 34)
and produces all the subkeys which depend ONLY on those known bits, it is
used only once, before the begining of the exhaustive search.

2. key4elim (PCF) - declared as "void key4elim(unsigned int uk[2])". This
function is used in the iteration on all the possibilities for key bits 35
to 64, it gets the full key for the current possibility (i.e. 1 to 34 -
known and 35 to 64 - curr. possib.) it produces all the remaining subkeys
)which also depend on key bits 35 to 64).

The Main function

Declared as "void main()", it works as follows:

1. It generates a Part A structures using PAF BuildSDB, then it runs PAF
ExludeAllBadKeys for each structure. This step terminates when there are
NO MORE then 2 possibilities for bits [1..24] are left (I've learned from
experience, then when you wait for remaining with only one possibility, it
takes an unnecessary long amount of time for some keys).

2. For each possibility for bits [1..24] of the key obtained in step (1), we
generate Part B structures using PBF BuildSDB, then we run PBF
ExludeAllBadKeys for each structure. This step terminates when we have NO
MORE then one possiblility for key bits [25..34] for each possibility for
key bits [1..24] obtained in step (1) (for each step (1) possibility we do
some "overkill" in Part B elimination to see if wrong possibilities
discriminate themselves by remaining without any possibility for key bits
[25..34], the detected here wrong possibilities are obviously discarded).

3. For each possibility of key bits [1..34] found in steps (1) and (2) (no
more then 2 possib., expected only one possib.) we perform an exhaustive
search for key bits [35..64], wrong possibilities obviously discard
themselves and we are left with only one possibility for the full 64-bit
key. Fast key generation functions (PCFs key4elimInit and key4elim) are
used in this step to speed-up the search. The expected complexity of the
exhaustive search is obviously O(2^30) (also the constant involved makes
it run a little slower then it seems).

4. Finally we are left with only one possibility for the full 64-bit key and
we report the results.

The obtained results

*In this section we will list the results obtained during the running of the

program IDEA_MIMA.exe (the implementation of the attack), which (together with

it's sourcecode: main.cpp) you can get from Appendix A. The resulting output

itself: results.txt can also be obtained from Appendix A.

The Results:

1. The program was run on Intel Pentium II 450 MHz computer, it took it
approximatly 1.3 hours to terminate, returning the correct 64-bit key.

2. The number of structures that were used:

· Part A used 35 structures = 35*2^16 CPs.

· Part B used 29 structures = 29*2^16 CPs.

· Part C used 2 KPs (for beter program readability, it could of
course use any of the previouse CPs).

3. Time listing:

· Part A took about about 40 minutes.

· Part B took 5-10 minutes.

· Part C (exhaustive search) took 30-35 minutes.

*The output of the program resides in a file named: "results.txt" and can be obtained in Appendix A.

Part IV: Study of a reduced variant of IDEA - XOR instead

of multiplication

Introduction

In this section we'll try to attend to another reduced variant of IDEA,

this variant differs is produced from the original IDEA by replacing all the

multiplication operations by XOR. From this point on we'll refer to this reduced

variant of the cipher by "IDEA_RV".

Key observations

1. Both bitwise XOR operation and addition modulu 2^n for 2 n-bit integers
have the following property:

· If we have two n-bit integers: X = (X1,x2,...,Xn) and Y = (Y1,Y2,...,Yn)
and we calculate: Z = (Z1,Z2,...,Zn) = (X1,X2,...,Xn) OP (Y1,Y2,...,Yn)
(where OP can be bitwise XOR or addition modulu 2^n) then for any
0<i<(n+1) Zi is affected only by X1,...,Xi and by Y1,...,Yi and IS NOT
affected by the higher then i bits of X and Y.

2. If we have a XOR differential of the type: d = (D1,D2,...,Di,0,...,0)
(last n-i bits are 0) (Remark: by "having" a differential I mean having a
pair X,Y, s.t. X XOR Y = d, and when we say that we add a constant to the
differential then we add it to X, add it to Y and then XOR the results
(i.e. in our notation if d = X XOR Y, then d+K = (XK) XOR (YK))),
then for any n-bit K, d+K’s las (n-i) bits will be 0 (obviouse from
observation (1)).

3. For two k-bit integers X and Y, P(XY = X+Y) =~ [2^k*(2^k-1)/2]/4^k =~
0.5 – 2^(-(k+1)) (i.e. probability of no carry is about 1/2 for large
enough k). For 1 bit X and Y, this probability is 3/4.

4. If we have 2 k-bit integers (k>=2): X and Y, let 1<=i<k, then if we
denote: Z= XY, then P([Zi XOR Z(i+1)]= [Xi XOR X(i+1) XOR Yi XOR
Y(i+1)])=3/4. This is easy to check if you denote the probability of carry
from addition of first i-1 bits (1 to (i-1)) of X and Y by p and calculate
the conditional probability of our event (Zi XOR Z(i+1)]= [Xi XOR X(i+1)
XOR Yi XOR Y(i+1)]), lets call it (*), conditioned on the appearance of
the carry, then when you add the probabilities (Bias rule) you’ll get:
P((*))=p*3/4+(1-p)*3/4=3/4.

5. If for two k-bit integers X and Y, d = X XOR Y = (1,0,...,0), then
IDEA_RV(X) XOR IDEA_RV(Y) = d =(1,0,...,0). It is obviouse, because if we
look on addition of 1 bit numbers (disreguarding the carry) then it’s hust
a XOR. This is TRUE for any k . This observation lets us distinguish
IDEA_RV from a random cipher with very high probability (2^(-k)) using
only 2 CPs (a pair of CPs that defer by d).

6. Similarly to 5, if we look on the rightmost bits of two integers then if
we add those integers then the rightmost bit of the result will be XOR of
the rightmostbit of the integers. (This observation gives us 4 bits of
IDEA_RVs key for free (obviouse)).

Attacks

1. Differential Cryptanalysis:

· The idea was suggested by Alex Biryukov, it is to try to start with
some “ugly” differential in the first round and try to get a nicer
differential (like something with many zeros at front) in the
following rounds, when you succeed, you’ll “feel” it in the output
(for instance if you have many zeros in front then because of the
low carry propagation probability (observation 3) there still be
many zeros in front at the output of IDEA_RV (that is if we work
with big blocks, 16-bit blocks are enough)) and then you’ll be able
to extract many bits of the key. I’ve tried to develop theis idea,
but I was unsuccessful for non-degenerate keys.

2. Linear Cryptanalysis:

· Using observation 4 as a linear approximation, we are left with a
linear approximation of the first 8 rounds of IDEA_RV with
“effective value” =~ 2^30*(3/4-1/2)^(4*7.5)=(1/2)^30 (by “effective
value” I mean the distance of the probability from 1/2). Thus
Matsui’s algorithm will require about 2^60 KPs if we use it.
Moreover there is a problem that also “theoreticly speaking” all the
bits of the relevant subkey are effective, but practicly, because of
the low probability of carry propagation (from rightmost bits to the
leftmost), there are only few “real effective bits” for the attack,
and thus this attack is unsuccessful.

3. Polynomial Approximation:

· This is my favorite approach. As we can see from observation 6, from
1 KP we already have 4 (XOR) equations “giving” us 4 bits of the
key. Afterwards, theoretically, another 2^8 CPs give us enough
equations to find all of the two rightmost bits of all the subkeys
(about 104). But it sounds vague and I’ve never tested this method
(it may be in fact, that as in the case of equations for the
rightmost bit, most of the equations will be degenerate and we’ll be
left with much fewer then 2^8 equations, but even then we’ll gain
some of the key bits). This approach can be extended further, but I
won’t do it here since I haven’t tested it.

References

1. "Miss in the Middle Attacks on IDEA, Khufu and Khafre" by E. Biham, A.
Biryukov and A. Shamir

2. "Chapter 3: The Block Cipher IDEA" from the book by Lai and Massey

Appendix A

1. Link to results.txt

2. Link to main.cpp

3. Link to IDEA_MIMA.exe