Overlapping Topologies



Next: Embedding in MPI
Up: Process Topologies
Previous: Virtual Topologies
topology, overlapping
In some applications, it is desirable to use different Cartesian topologies at
different stages in the computation. For example, in a QR
factorization, the 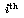 transformation is determined by the
data below the diagonal in the
transformation is determined by the
data below the diagonal in the 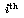 column of the matrix. It
is often easiest to think of the upper right hand corner of the 2D
topology as starting on the process with the
column of the matrix. It
is often easiest to think of the upper right hand corner of the 2D
topology as starting on the process with the 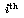 diagonal
element of the matrix for the
diagonal
element of the matrix for the 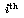 stage of the computation.
Since the original matrix was laid out in the original 2D topology, it
is necessary to maintain a relationship between it and the shifted 2D
topology in the
stage of the computation.
Since the original matrix was laid out in the original 2D topology, it
is necessary to maintain a relationship between it and the shifted 2D
topology in the 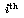 stage. For example, the processes
forming a row or column in the original 2D topology must also form a
row or column in the shifted 2D topology in the
stage. For example, the processes
forming a row or column in the original 2D topology must also form a
row or column in the shifted 2D topology in the 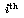 stage.
As stated in Section
stage.
As stated in Section 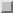 and shown in
Figure
and shown in
Figure  , there is a clear correspondence between
the rank of a process and its coordinates in a Cartesian topology.
This relationship can be used to create multiple Cartesian topologies
with the desired relationship. Figure
, there is a clear correspondence between
the rank of a process and its coordinates in a Cartesian topology.
This relationship can be used to create multiple Cartesian topologies
with the desired relationship. Figure  shows
the relationship of two 2D Cartesian topologies where the second
one is shifted by two rows and two columns.
shows
the relationship of two 2D Cartesian topologies where the second
one is shifted by two rows and two columns.
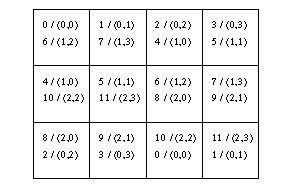
Figure: The relationship between two overlaid topologies on a
3x4 torus. The upper values in each process is the
rank / (row,col) in the original 2D topology and the lower values are
the same for the shifted 2D topology. Note that rows and columns of
processes remain intact.
Jack Dongarra
Fri Sep 1 06:16:55 EDT 1995
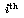 transformation is determined by the
data below the diagonal in the
transformation is determined by the
data below the diagonal in the 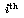 column of the matrix. It
is often easiest to think of the upper right hand corner of the 2D
topology as starting on the process with the
column of the matrix. It
is often easiest to think of the upper right hand corner of the 2D
topology as starting on the process with the 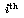 diagonal
element of the matrix for the
diagonal
element of the matrix for the 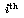 stage of the computation.
Since the original matrix was laid out in the original 2D topology, it
is necessary to maintain a relationship between it and the shifted 2D
topology in the
stage of the computation.
Since the original matrix was laid out in the original 2D topology, it
is necessary to maintain a relationship between it and the shifted 2D
topology in the 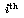 stage. For example, the processes
forming a row or column in the original 2D topology must also form a
row or column in the shifted 2D topology in the
stage. For example, the processes
forming a row or column in the original 2D topology must also form a
row or column in the shifted 2D topology in the  stage.
As stated in Section
stage.
As stated in Section 