If the process topology is a Cartesian structure, a MPI_SENDRECV operation is likely to be used along a coordinate direction to perform a shift of data. As input, MPI_SENDRECV takes the rank of a source process for the receive, and the rank of a destination process for the send. A Cartesian shift operation is specified by the coordinate of the shift and by the size of the shift step (positive or negative). The function MPI_CART_SHIFT inputs such specification and returns the information needed to call MPI_SENDRECV. The function MPI_CART_SHIFT is local.

MPI_Cart_shift(MPI_Comm comm, int direction, int disp, int *rank_source, int *rank_dest)
MPI_CART_SHIFT(COMM, DIRECTION, DISP, RANK_SOURCE, RANK_DEST, IERROR)INTEGER COMM, DIRECTION, DISP, RANK_SOURCE, RANK_DEST, IERROR
The direction argument indicates the dimension of the shift, i.e., the coordinate whose value is modified by the shift. The coordinates are numbered from 0 to ndims-1, where ndims is the number of dimensions.
Depending on the periodicity of the Cartesian group in the specified coordinate direction, MPI_CART_SHIFT provides the identifiers for a circular or an end-off shift. In the case of an end-off shift, the value MPI_PROC_NULL may be returned in MPI_PROC_NULL rank_source and/or rank_dest, indicating that the source and/or the destination for the shift is out of range. This is a valid input to the sendrecv functions.
Neither MPI_CART_SHIFT, nor MPI_SENDRECV are
collective functions. It is not required that all processes in the
grid call MPI_CART_SHIFT with the same direction
and disp arguments, but only that sends match receives in the
subsequent calls to MPI_SENDRECV.
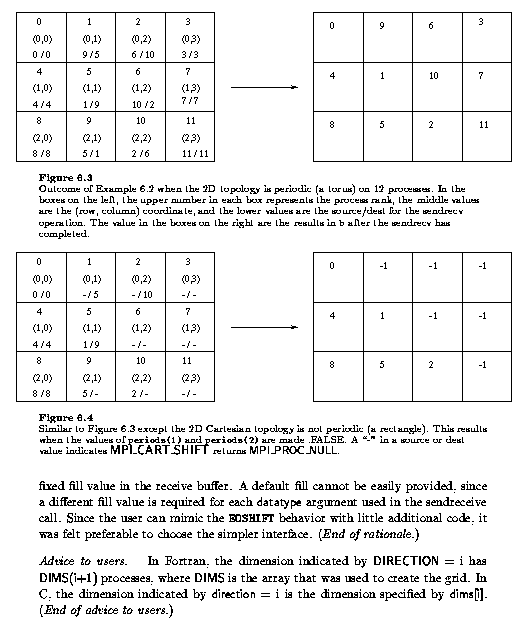
Example ![]() shows such use of MPI_CART_SHIFT,
where each column of a 2D grid is shifted by a different amount.
Figures
shows such use of MPI_CART_SHIFT,
where each column of a 2D grid is shifted by a different amount.
Figures ![]() and
and ![]() show the
result on 12 processors.
show the
result on 12 processors.