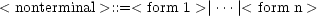
The syntax of a programming language is the set of rules governing the formation of expressions in the language. The semantics of a programming language is the meaning of those expressions.
There are several forms of language semantics. Axiomatic semantics is a set of axiomatic truths in a programming language. Denotational semantics involves modeling programs as static mathematical objects, namely as set-theoretic functions with specific properties. We, however, will focus on a form of semantics called operational semantics.
An operational semantics is a mathematical model of programming language execution. It is, in essence, an interpreter defined mathematically. However, an operational semantics is more precise than an interpreter because it is defined mathematically, and not based on the meaning of the language in which the interpreter is written. Formally, we can define operational semantics as follows.
Definition 2.1 (Operational Semantics). An operational semantics for a programming language is a mathematical definition of its computation relation, e ==> v, where e is a program in the language.
e ==> v is mathematically a 2-place relation between expressions of the language, e, and values of the language, v. Integers and booleans are values. Functions are also values because they don’t compute to anything. e and v are metavariables, meaning they denote an arbitrary expression or value, and should not be confused with the (regular) variables that are part of programs.
An operational semantics for a programming language is a means for understanding in precise detail the meaning of an expression in the language. It is the formal specification of the language that is used when writing compiles and interpreters, and it allows us to rigorously verify things about the language.
Backus-Naur Form (BNF) grammars are a standard formalism for defining language syntax.. All BNF grammars comprise terminals, nonterminals (aka syntactic categories), and production rules, the general form of which is:
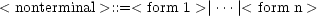
example The language SHEEP. Let {S} be the set of nonterminals, {a,b} be the set of terminals, and the grammar definition be:
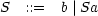


example The language FROG. Let {F,G} be the set of nonterminals, {r,i,b,t} be the set of terminals, and the grammar definition be:
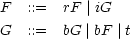

In order to get a feel for what an operational semantics is and how it is defined, we will now examine the operational semantics for a very simple language: boolean logic with no variables. The syntax of this language is as follows. An expression e is recursively defined to consist of the values True and False, and the expressions e And e, e Or e, e Implies e, and Not e.1 This syntax is known as the concrete syntax, because it is the syntax that describes the textual representation of an expression in the language. We can express it in a BNF grammar as follows:
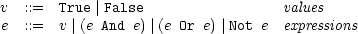
Another form of syntax, the abstract syntax, is an representation of an expression in the form of a syntax tree. These abstract syntax trees are used internally by interpreters or compilers to process expressions in the language. These two forms of syntax are discussed thoroughly in Section 2.3.1. We can represent the abstract syntax of our boolean language through the Caml type below.
Let us take a look at a few examples to see how the concrete and the abstract syntax relate.
|
|
|
Again, we will come back to the issue of concrete and abstract syntax shortly.
Here is a full inductive definition of a translation from the concrete to the
abstract syntax:
| JTrueK | = | True |
| JFalseK | = | False |
| JeK | = | Not(JeK) |
| Je1 And e2K | = | And(Je1K, Je2K) |
| Je1 Or e2K | = | Or(Je1K, Je2K) |
Now we are ready to define the operational semantics of our boolean language to be the least relation ==> satisfying the following rules:
| (True Rule) |
| |||
| (False Rule) |
| |||
| (Not Rule) |
| |||
| (And Rule) |
|
These rules form a proof system in analogy to logical rules. The horizontal line reads “implies”. Thus rules represent logical truths. It follows that rules with nothing above the line are axioms since they always hold. A proof of e ==> v amounts to constructing a sequence of rule applications for which the final rule application logically concludes with e ==> v. We define the operational semantics as the “least relation” satisfying these rules, where “least” means “fewest pairs related”. Without this requirement, a relation which related anything to anything would be valid. For example,
| Not(Not False) And True ==> False, because by the And rule |
| True ==> True, and |
| Not(Not False) ==> False, the latter because |
| Not False ==> True, because |
| False ==> False. |
This computation is a tree because there are two subcomputations for each binary operator.
Exercise 2.1. Complete the definition of the operational semantics for the boolean language described above by writing the rules for Or and Implies
An advantage of an operational semantics is that is allows us to prove things about the execution of programs. For example, we may make the following claims about the boolean language:
Proof. By induction on the height of the proof tree.
Lemma 2.2. The boolean language is normalizing: For all boolean expressions e, there is some value v where e ==> v.
Proof. By induction on the size of e.
There is a very close relationship between an operational semantics and an actual interpreter written in Caml. Given an operational semantics defined via the relation ==> , there is a corresponding (Caml) evaluator function eval.
Definition 2.2 (Faithful Implementation). A (Caml) interpreter function eval faithfully implements an operational semantics e ==> v if the following is true. e ==> v if and only if eval(e) returns result v.
The operational semantics rules for the boolean language above induces the following Caml interpreter eval function.
The only difference between the operational semantics and the interpreter is that the interpreter is a function, so we start with the bottom-left expression in a rule, use the interpreter to recursively produce the value(s) above the line in the rule, and finally compute and return the value below the line in the rule.
Note that the boolean language interpreter above faithfully implements its operational semantics: e ==> v if and only if eval(e) returns v as result. We will go back and forth between these two forms throughout the book. The operational semantics form is used because it is independent of any particular programming language. The interpreter form is useful because it can be tested on real code.
Definition 2.3 (Metacircular Interpreter). A metacircular interpreter is an interpreter for (possibly a subset of) a language x that is written in language x.
Metacircular interpreters give you some idea of how a language works, but suffer from the non-foundational problems implied in Exercise 2.2. A metacircular interpreter for Lisp is a classic programming language theory exercise.
Now that we have seen how to define and understand operational semantics, we will begin to study our first programming language: D. D is a “Diminutive” pure functional programming language. It has integers, booleans, and higher-order anonymous functions. In most ways D is much weaker than Caml: there are no reals, lists, types, modules, state, or exceptions.
D is untyped, and in this way is it actually more powerful than Caml. It is possible to write some programs in D that produce no runtime errors, but which will not typecheck in Caml. For instance, our encoding of recursion in Section 2.3.5 is not typeable in Caml. Type systems are discussed in Chapter 6. Because there are no types, runtime errors can occur in D, for example the application (5 3).
Although it is very simplistic, D is still Turing-complete: every partial recursive function on numbers can be written in D. In fact, it is even Turing-complete without numbers or booleans. This language with only functions and application is known as the pure lambda-calculus, and is discussed briefly in Section 2.4.3. No deterministic programming language can compute more than the partial recursive functions.
As we said earlier, the syntax of a language is the set of rules governing the formation of expressions in that language. However, there are different but equivalent ways to represent the same expressions, and each of these ways is described by a different syntax.
As mentioned in the presentation of the boolean language, the syntax has two forms, concrete syntax that is the textual representation, and the abstract syntax which is the syntax tree representation of the concrete syntax. In our interpreters, the abstract syntax is the Caml value of some type expr that represents the program.
Let us begin by defining the concrete syntax of D. The expressions, e, of D are defined by the following BNF:

Note, the metavariables we are using include e meaning an arbitrary D expression, v meaning an arbitrary value expression, and x meaning an arbitrary variable expression. Be careful about that last point. It does not claim that all variables are metavariables, but rather x is a metavariable representing an arbitrary D variable.
To define the abstract syntax of D for a Caml interpreter, we need to define a variant type that captures the expressiveness of D. The variant type we will use is as follows.
One important point here is the existence of the ident type. Notice where ident is used in the expr type: as variable identifiers, and as function parameters for Function and Let Rec. What ident is doing here is enforcing the constraint that function parameters may only be variables, and not arbitrary expressions. Thus, Ident "x" represents a variable declaration and Var(Ident "x") represents a variables usage.
Being able to convert from abstract to concrete syntax and vice versa is an important skill for one to develop, however it takes some time to become proficient at this conversion. Let us look as some examples D. In the examples below, the concrete syntax is given at the top, and the the corresponding abstract syntax representation is given underneath.
|
|
|
|
|
Notice how lengthy even simple expressions can become when represented in the abstract syntax. Review the above examples carefully, and try some additional examples of your own. It is important to be able to comfortably switch between abstract and concrete syntax when writing compilers and interpreters.
The main feature of D is higher-order functions, which also introduces variables. Recall that programs are computed by rewriting them:
| (Function x -> x + 2)(3 + 2 + 5) ==> 12 because |
| 3 + 2 + 5 ==> 10, because |
| 3 + 2 ==> 5, and |
| 5 + 5 ==> 10; and then, |
| 10 + 2 ==> 12. |
Note how in this example, the argument is substituted for the variable in the body--this gives us a rewriting interpreter. In other words, D functions compute by substituting the actual argument for the for parameter; for example,
(Function x -> x + 1) 2
will compute by substituting 2 for x in the function’s body x + 1, i.e. by computing 2 + 1. We need to be careful about how variable substitution is defined. For instance,
(Function x -> Function x -> x) 3
should not evaluate to Function x -> 3 since the inner x is bound by the inner parameter. To correctly formalize this notion, we need to make the following definitions.
Definition 2.4 (Variable Occurrence). A variable use x occurs in e if x appears somewhere in e. Note we refer only to variable uses, not definitions.
Definition 2.5 (Bound Occurrence). Any occurrences of variable x in the expression
Function x -> e
are bound, that is, any free occurrences of x in e are bound occurrences in this expression. Similarly, in the expression
Let Rec f x =e1 In e2
occurrences of f and x are bound in e1 and occurrences of f are bound in e2. Note that x is not bound in e2, but only in e1, the body of the function.
Definition 2.6 (Free Occurrence). A variable x occurs free in e if it has an occurrence in e which is not a bound occurrence.
Let’s look at a few examples of bound versus free variable occurrences.
|
|
|
Definition 2.7 (Closed Expression). An expression e is closed if it contains no free variable occurrences. All programs we execute are closed (no link-time errors).
Of the examples above, Examples 2.10 and 2.12 are closed expressions, and Example 2.11 is not a closed expression.
Definition 2.8 (Variable Substitution). The variable substitution of x for e' in e, denoted e[e'/x], is the expression resulting from the operation of replacing all free occurrences of x in e with e'. For now, we assume that e' is a closed expression.
Here is an equivalent inductive definition of substitution:
![x[v/x] = v
x'[v/x] = x' x /= x'
(Function x-- > e)[v/x] = (Function x --> e)
(Function x'--> e)[v/x] = (Function x'--> e[v/x]) x /= x'
n[v/x] = n for n (- Z
True[v/x] = True
False[v/x] = False
(e1 + e2)[v/x] = e1[v/x]+ e2[v/x]
(e1 And e2)[v/x] = e1[v/x] And e2[v/x]
...](main8x.gif)
| Let Rec f x = |
| If x = 1 Then |
| (Function f -> f (x - 1)) (Function x -> x) |
| Else |
| f (x - 1) |
| In f 100 |
How does this expression evaluate? It is a bit difficult to tell simply by looking at it because of the tricky bindings. Let’s figure out what variable occurrences are bound to which function declarations and rewrite the function in a clearer way. A good way to do this is to choose new, unambiguous names for each variable, taking care to preserve bindings. We can rewrite the expression above as follows.
| Let Rec x1 x2 = |
| If x2 = 1 Then |
| (Function x3 -> x3 (x2 - 1)) (Function x4 -> x4) |
| Else |
| x1 (x2 - 1) |
| In x1 100 |
Now it’s much easier to figure out the result. You may wish to read Section 2.3.3, which discusses the operational semantics of D, before trying it. At any rate, notice that the recursive case (the else-clause) simply applies x1 to (x2 - 1), where x2 is the argument to x1. So eventually, x1 100 simply evaluates the the base case of the recursion. In the base case, the then-clause, an identity function (Function x4 -> x4) is passed to a function that applies it to x2 - 1, which is always 0 in the base case. Therefore, we know that x1 100 ==> 0.
We are now ready to define the operational semantics for D. As before, the operational semantics of D is defined as the least relation ==> on closed expressions in D satisfying the following rules.
| (Value Rule) |
| |||
| (+ Rule) |
| |||
| (= Rule) |
| |||
| (If True Rule) |
| |||
| (If False Rule) |
| |||
| (Application Rule) |
|
| (Let Rec) |
|
For brevity we have left out a few rules. The - rule is similar to the + rule. The rules on boolean operators are the same as those given in Section 2.2.1.
There are several points of interest in the above rules. First of all, notice that the function application rule is defined as call-by-value; the argument is evaluated before the function is applied. Later we discuss other possibilities: call-by-name and call-by-reference parameter passing. Call-by-reference parameter passing is irrelevant for languages, such as D, that contain no mutable store operations (such languages are discussed in Chapter 3).
Another thing to note in the rules is that there are two If rules: one for the case that the condition is true and one for the case that the condition is false. It may seem that we could combine these two rules into a single one, but look closely. If the condition is true, only the expression in the Then clause is evaluated, and if the condition is false, only the expression in the Else clause is evaluated. To see why we do not want to evaluate both clauses, consider the following D expression.
If True Then 1 Else (0 1)
This code should not result in a run-time error, but if we were to evaluate both clauses a run-time error would certainly occur when (0 1) is evaluated. In addition, if our language has state (see Chapter 3), evaluating both clauses may produce unintended side-effects.
Here are a few derivation examples; these proofs are written in goal-directed style, starting with the last line. In other words, the root of the tree is at the top. Sub-nodes of the tree are indented.
| If 3 = 4 Then 5 Else 4 + 2 ==> 6 because |
| 3 = 4 ==> False and |
| 4 + 2 ==> 6, because |
| 4 ==> 4 and |
| 2 ==> 2 and 4 plus 2 is 6. |
| (Function x -> If 3 = x Then 5 Else x + 2) 4 ==> 6, by above derivation |
| (Function x -> x x)(Function y -> y) ==> Function y -> y, because |
| (Function y -> y)(Function y -> y) ==> Function y -> y |
| (Function f -> Function x -> f(f(x)))(Function x -> x - 1) 4 ==> 2 |
| because letting F abbreviate (Function x -> x - 1) |
| (Function x -> F(F(x))))) 4 ==> 2, because |
| F(F 4) ==> 2, because |
| F 4 ==> 3, because |
| 4 - 1 ==> 3. And then, |
| F(3) ==> 2, because |
| 3 - 1 ==> 2 |
| (Function x -> Function y -> x + y) |
| ((Function x -> If 3 = x Then 5 Else x + 2) 4) |
| ((Function f -> Function x -> f (f x)) |
| (Function x -> x - 1) 4) ==> 8 by the above two executions |
Finally, the Let Rec rule merits some discussion. This rule is a bit difficult to grasp at first because of the double substitution. Let’s break it down. The outermost substitution “unrolls” one level of the recursion by translating it to a function whose argument is x, the argument of the Let Rec statement. However, if we stopped there, we would just have a regular function, and f would be unbound. We need some mechanism that actually gets us the recursion. That’s where the inner substitution comes into play. The inner substitution replaces f with the expression Let Rec f x = e1 In f. Thus, the Let Rec rule is inductively defined: the body of the Let Rec expression is replaced with a value that contains a Let Rec. The inductive definition of the rule is where the recursion comes from.
To fully understand why this rule is correct, we need to look at an execution. Consider the following expression.
| Let Rec f x = |
| If x = 1 Then 1 Else x + f (x - 1) |
| In f 3 |
The expression is a recursive function that sums the numbers 1 through x, therefore the result of f 3 should be 6. We’ll trace through the evaluation, but for brevity we will not write out every single step. Let
body = If x = 1 Then 1 Else x + f (x - 1).
Then
| Let Rec f x = body In f 3 ==> 6, because |
| (Function x -> If x = 1 Then 1 Else x + |
| (Let Rec f x = body In f) (x - 1)) 3 ==> 6, because |
| 3 + (Let Rec f x = body In f) 2 ==> 6, because |
| (Let Rec f x = body In f) 2 ==> 3, because |
| (Function x -> If x = 1 Then 1 Else x + |
| (Let Rec f x = body In f) (x - 1)) 2 ==> 3, because |
| 2 + (Let Rec f x = body In f) 1 ==> 3, because |
| (Let Rec f x = body In f) 1 ==> 1, because |
| (Function x -> If x = 1 Then 1 Else x + |
| (Let Rec f x = body In f) (x - 1)) 1 ==> 1 |
|
As we mentioned before, one of the main benefits of defining an operational semantics for a language is that we can rigorously verify claims about that language. Now that we have defined the operational semantics for D, we can prove a few things about it.
Proof. By inspection of the rules, at most one rule can apply at any time.
Proof. To show that a language is not normalizing, we simply show that there is some e such that there is no v with e ==> v.
(Function x -> x x)(Function x -> x x)
is not normalizing. This is a very interesting expression that we will look at in more
detail in Section 2.3.5. (4 3) is a simpler expression that is not normalizing.
D doesn’t have many features, but it is possible to do much more than it may seem. As we said before, D is Turing complete, which means, among other things, that any Caml operation may be encoded in D. We can informally represent encodings in our interpreter as macros using Caml let statements. A macro is equivalent to a statement like “let F be Function x -> ...”
Logical Combinators First, there are the classic logical combinators, simple functions for recombining data.
| combI = Function x -> x |
| combK = Function x -> Function y -> x |
| combS = Function x -> Function y -> Function z -> (x z) (y z) |
| combD = Function x -> x x |
Tuples Tuples and lists are encodable from just functions, and so they are not needed as primitives in a language. Of course for an efficient implementation you would want them to be primitives, thus doing this encoding is simply an exercise to better understand the nature of functions and tuples. We will define a 2-tuple (pairing) constructor; From a pair you can get a n-tuple by building it from pairs. For example, (1,(2,(3,4))) represents the 4-tuple (1,2,3,4).
First, we need to define a pair constructor, pr. A first approximation of the constructor is as follows.
pr (l, r) = Function x -> x l r
Then, the operations for left and right projections may be defined.
| left (e) = e (Function x -> Function y -> x) |
| right (e) = e (Function x -> Function y -> y) |
Now let’s take a look at what’s happening. pr takes a left expression, l, and a right expression, r, and packages them into a function that applies its argument x to l and r. Because functions are values, the result won’t be evaluated any further, and l and r will be packed away in the body of the function until it is applied. Thus pr succeeds in “storing” l and r.
All we need now is a way to get them out. For that, look at how the projection operations left and right are defined. They’re both very similar, so let’s concentrate only on the projection of the left element. left takes one of our pairs, which is encoded as a function, and applies it to a curried function that returns its first, or leftmost, element. Recall that the pair itself is just a function that applies its argument to l and r. So when the curried left function that was passed in is applied to l and r, the result is l, which is exactly what we want. right is similar, except that the curried function returns its second, or rightmost, argument.
Before we go any further, there is a technical problem involving our encoding of pr. Suppose l or r contain a free occurrence of x when pr is applied. Because pr is defined as Function x -> x l r, any free occurrence x contained in l or r will become bound by x after pr is applied. This is known as variable capture. To deal with capture here, we need to change our definition of pr to the following.
pr (l, r) = (Function l -> Function r -> Function x -> x l r) l r
This way, instead of textually substituting for l and r directly, we pass them in as functions. This allows the interpreter evaluate l and r to values before passing them in, and also ensures that l and r are closed expressions. This eliminates the capture problem, because any occurrence of x is either bound by a function declaration inside l or r, or was bound outside the entire pr expression, in which case it must have already been replaced with a value at the time that the pr subexpression is evaluated. Variable capture is an annoying problem that we will see again in Section 2.4.
Now that we have polished our definitions, let’s look at an example of how to use these encodings. First, let’s create create the pair p as (4,5).
p = pr (4, 5) ==> Function x -> x 4 5
Now, let’s project the left element of p.
left p = (Function x -> x 4 5) (Function x -> Function y -> x)
This becomes
(Function x -> Function y -> x) 4 5 ==> 4.
This encoding works, and has all the expressiveness of real tuples. There are, nonetheless, a few problems with it. First of all, note that
left (Function x -> 0) ==> 0.
We really want the interpreter to produce a run-time error here, because a function is not a pair.
Similarly, suppose we wrote the program (pr (3, pr (4, 5))). One would expect this expression to evaluate to pr (4, 5), but remember that pairs are not values in our language, but simply encodings, or macros. So in fact, the result of the computation is Function x -> x 4 5. We can only guess that this is intended to be a pair. In this respect, the encoding is flawed, and we will, in Chapter 3, introduce “real” n-tuples into an extension of D to alleviate these kinds of problems.
Lists Lists can also be implemented via pairs. In fact, pairs of pairs are technically needed because we need a flag to mark the end of list. The list [1; 2; 3] is represented by pr (pr(false,1), pr (pr(false,2), pr (pr(false,3), emptylist))) where emptylist pr(pr(true,0),0). The true/false flag is used to mark the end of the list: only the empty list is flagged true. The implementation is as follows.
| cons (x, y) = pr(pr(Bool false, x), y) |
| emptylist = pr(pr(Bool true, Int 0),Int 0) |
| head x = right(left x) |
| tail x = right x |
| isempty l = (left (left l)) |
| length = Let Rec len x = |
| If isempty(x) Then 0 Else 1 + len (tail x) In len |
Functions with Multiple Arguments Functions with multiple arguments are done with currying just as in Caml. For example
Function x -> Function y -> x + y
The Let Operation Let is quite simple to define in D.
(Let x = e In e') = (Function x -> e') e
For example,
(Let x = 3 + 2 In x + x) = (Function x -> x + x) (3 + 2) ==> 10.
Sequencing Notice that D has no sequencing (;) operation. Because D is a pure functional language, writing e; e' is really just equivalent to writing e', since e will never get used. Hence, sequencing really only has meaning in languages with side-effects. Nonetheless, sequencing is definable in the following manner.
e; e' = (Function n -> e') e,
where n is chosen so as not to be free in e'. This will first execute e, throw away the value, and then execute e', returning its result as the final result of e; e'.Freezing and Thawing We can stop and re-start computation at will by freezing and thawing.
| Freeze e = Function n -> e |
| Thaw e = e 0 |
Let x = Freeze (2 + 3) In (Thaw x) + (Thaw x)
This expression has same value as the equivalent expression without the freeze and thaw, but the 2 + 3 is evaluated twice. Again, in a pure functional language the only difference is that freezing and thawing is less efficient. In a language with side-effects, if the frozen expression causes a side-effect, then the freeze/thaw version of the function may produce results different from those of the original function, since the frozen side-effects will be applied as many times as they are thawed.
D has a built-in Let Rec operation to aid in writing recursive functions, but its actually not needed because recursion is definable in D. The encoding is a non-obvious one, and so before we introduce it, we present some background information. As we will see, the encoding of recursion is closely related to a famous set-theoretical paradox due to Russell.
Let us begin by posing the following question. How can programs compute forever in D without recursion? The answer to this question comes in the form of a seemingly simple expression:
(Function x -> x x)(Function x -> x x)
Recall from Lemma 2.2, that a corollary to the existence of this expression is that D is not normalizing. This computation is odd in some sense. (x x) is a function being applied to itself. There is a logical paradox at the heart of this non-normalizing computation, namely Russell’s Paradox.
In Frege’s set theory (circa 1900), sets were written as predicates P(x), which we can view as functions. In the functional view, set membership is via application:
e in S iff S (e) ==> True
For example, (Function x -> x < 2) is the set of all numbers less than 2. The integer 1 is in this “set”, since (Function x -> x < 2) 1 ==> True.
Russell discovered a paradox in Frege’s set theory, and it can be expressed in the following way.
Definition 2.9 (Russell’s Paradox). Let P be the set of all sets that do not contain themselves as members. Is P a member of P?
Asking whether or not a set is a member of itself seems like strange question, but in fact there are many sets that are members of themselves. The infinitely receding set {{{{...}}}} has itself as a member. The set of things that are not apples is also a member of itself (clearly, a set of non-apples is not an apple). These kinds of sets arise only in “non-well-founded” set theory.
To explore the nature of Russell’s Paradox, let us try to answer the question it poses: Does P contain itself as a member? Suppose the answer is yes, and P does contain itself as a member. If that were the case then P should not be in P, which is the set of all sets that do not contain themselves as members. Suppose, then, that the answer is no, and that P does not contain itself as a member. Then P should have been included in P, since it doesn’t contain itself. In other words, P is a member of P if and only if it isn’t. Hence Russell’s Paradox is indeed a paradox. Let us now rephrase the paradox using D functions instead of predicates.
Definition 2.10 (Computational Russell’s Paradox). Let
P = Function x -> Not(x x).
What is the result of P P? Namely, what is
(Function x -> Not(x x)) (Function x -> Not(x x))?
If this D program were evaluated, it would run forever. To see this, it suffices to compute one step of the evaluation, and notice that the inner expression has not been reduced.
Not(((Function x -> Not(x x)) (Function x -> Not(x x)))
Again, this statement tells us that P P ==> True if and only if P P ==> False. This is not how Russell viewed his paradox, but it has the same core structure, only it is rephrased in terms of computation, and not set theory. The computational realization of the paradox is that the predicate doesn’t compute to true or false, so its not a sensible logical statement. Russell’s discovery of this paradox in Frege’s set theory shook the foundations of mathematics. To solve this problem, Russell developed his ramified theory of types, which is the ancestor of types in programming languages. The program
is not typeable in Caml for the same reason the corresponding predicate is not typeable in Russell’s ramified theory of types. Try typing the above code into the Caml top-level and see what happens.
More information on Russell’s Paradox may be found in [14].
In the logical view, passing a function to itself as argument is a bad thing. From a programming view, however, it can be an extremely powerful tool. Passing a function to itself allows recursive functions to be defined, without Let Rec.
The idea is as follows. In a recursive function, two identical copies of the function are maintained: one to use, and one to copy again. When a recursive call is made, one copy of the function is passed along. Inside the recursive call, two more copies are made. One of these copies is used to do computation, and the other is saved for a future recursive call. The computation proceeds in this way until the base case of the recursion occurs, at which point the function returns.
Let us make this method a little clearer by looking at an example. We wish to write a recursive summate function that sums the integers {0,1,...,n} for argument n. We first define
| summate0 = Function this -> Function arg -> |
| If arg = 0 Then 0 Else arg + this this (arg - 1) |
Then we can write a function call as
summate0 summate0 7
which computes the sum of the integers {0,1,...,7}. summate0 always expects its first argument this to be itself. It can then use one copy for the recursive call (the first this) and pass the other copy on for future duplication. So summate0 summate0 “primes the pump”, so to speak, by giving the process an initial extra copy of itself. In general, we can write the whole thing in D as
| summate = Let summ = Function this -> Function arg -> |
| If arg = 0 Then 0 Else arg + this this (arg - 1) |
| In Function arg -> summ summ arg |
and invoke as simply summate 7 so we don’t have to expose the self-passing.
The Y -Combinator The Y -combinator is a further abstraction of self-passing. The idea is that the Y -combinator does the self-application with an abstract body of code that is passed in as an argument. We first define a function called almost_y, and then revise that definition to arrive at the real Y -combinator.
| almost_y = Function body -> |
| Let fun = Function this -> Function arg -> |
| body this arg |
| In Function arg -> fun fun arg |
using almost_y, we can define summate as follows.
| summate = almost_y (Function this -> Function arg -> |
| If arg = 0 Then 0 Else arg + this this (arg - 1)) |
The true Y -combinator actually goes one step further and passes this (this) as argument, not just this, simplifying what we pass to Y :
Definition 2.11 (Y -Combinator).
| combY = Function body -> |
| Let fun = Function this -> Function arg -> |
| body (this this) arg |
| In Function arg -> fun fun arg |
The Y -combinator can then be used to define summate as
| summate = combY (Function this -> Function arg -> |
| If arg = 0 Then 0 Else arg + this (arg - 1)) |
In call-by-name parameter passing, the argument to the function is not evaluated at function call time, but rather is only evaluated if it is used. This style of parameter passing is largely of historical interest now, Algol uses it but no modern languages do. The reason is that it is much harder to write efficient compilers if call-by-name parameter passing is used. Nonetheless, it is worth taking a brief look at call-by-name parameter passing.
Let us define the operational semantics for call-by-name.
| (Call-By-Name Application) |
|
Freezing and thawing, defined in Section 2.3.4, is a way to get call-by-name behavior in a call-by-value language. Consider, then, the computation of
(Function x -> Thaw x + Thaw x) (Freeze (3 - 2))
(3 - 2) is not evaluated until we are inside the body of the function where it is thawed, and it is then evaluated two separate times. This is precisely the behavior of call-by-name parameter passing, so Freeze and Thaw can encode it by this means. The fact that (3 - 2) is executed twice shows the main weakness of call by name, namely repeated evaluation of the function argument.
Lazy or call-by-need evaluation is a version of call-by-name that caches evaluated function arguments the first time they are evaluated so it doesn’t have to re-evaluate them in subsequent uses. Haskell [13, 6] is a pure functional language with lazy evaluation.
One of the most basic operations defined over a space of mathematical objects is the equivalence relation. Equivalence makes sense for programs too, and we will give it some treatment in this section.
Defining an equivalence relation, =~, for programs is actually not as straightforward as one might expect. The initial idea is to define the relation such that two programs are equivalent if they always lead to the same results when used. As we will see, however, this definition is not sufficient, and we will need to do some work to arrive at a satisfactory definition.
Let us begin by looking at a few sample equivalences to get a feel for what they are. eta-conversion is one example of an interesting equivalence. It is defined as follows.
| Function x -> e =~ |
| Function z -> (Function x -> e) z, for z not free in e |
eta-conversion is similar to the proxy pattern in object oriented programming[11]. A closely related law for our freeze/thaw syntax is
Thaw (Freeze e) =~ e
In both examples, one of the expressions may be replaced by the other without ill effects (besides perhaps changing execution time), so we say they are equivalent. We will need to develop a more rigorous definition of equivalence, though.
Equivalence is an important concept because it allows programs to be transformed by replacing bits with equal bits and the programmer need not even be told since the observed behavior will be the same. Thus, they are transformations that can be performed by a compiler, and operational equivalence provides a rigorous foundation for compiler optimization.
Let’s begin by informally strengthening our definition of operational equivalence. We define equivalence in a manner dating all the way back to Leibniz[18]:
Definition 2.12 (Operational Equivalence (Informal)). Two programs are equivalent if and only if one can be replaced with the other at any place, and no external change in behavior will be noticed.
We wish to study equivalence for possibly open programs, because there are good equivalences such as x + 1 - 1 =~ x. We define “at any place” by the notion of a program context, which is, informally, a D program with some holes (*) in it. Using this informal definition, testing if e1 =~ e2 would be roughly equivalent to performing the following steps (for all possible programs and all possible holes, of course).
Now let us elaborate on the notion of a program context. Take a D program with some “holes” (*) punched in it: replace some subterms of any expression with *. Then “hole-filling” in this program context C, written C[e], means replacing * with e in C. Hole filling is like substitution, but without the concerns of bound or free variables. It is direct replacement with no conditions.
Let us look at an example of contexts and hole-filling using eta-conversion as we defined above. Let
C = (Function z -> Function x -> *) z
Now, filling the hole with x + 2 is simply written
| ((Function z -> Function x -> *) z)[x + 2] = |
| (Function z -> Function x -> x + 2) z |
Finally, we are ready to rigorously define operational equivalence.
Definition 2.13 (Operational Equivalence). e =~ e' if and only if for all contexts C, C[e] ==> v for some v if and only if C[e'] ==> v' for some v'.
Another way to phrase this definition is that two expressions are equivalent if in any possible context, C, one terminates if the other does. We call this operational equivalence because it is based on the interpreter for the language, or rather it is based on the operational semantics. The most interesting, and perhaps nonintuitive, part of this definition is that nothing is said about the relationship between v and v'. In fact, they may be different in theory. However, intuition tells us that v and v' must be very similar, since their equivalence hold for any possible context.
For example, to prove that 2 =/~ 3, we must demonstrate a context C such that C[2] ==> v and C[3] =/=> v' for any v' in the language. One possible C is
C = Let Rec fun x = If x = 2 Then 0 Else fun x In fun *
Then clearly, C[2] ==> 2 and C[3] =/=> v for any v.
The only problem with this definition of equivalence is its “incestuous” nature--there is no absolute standard of equivalence removed from the language. Domain theory is a mathematical discipline which defines an algebra of programs in terms of existing mathematical objects (complete and continuous partial orders). We are not going to discuss domain theory here, mainly because it does not generalize well to programming languages with side effects. [16] explores the relationship between operational semantics and domain theory.
In this section, we present some general equivalence principles for in D.
Definition 2.18 (Beta-Equivalence).
((Function x -> e) v) =~ (e{v/x})
where e{v/x} is the capture-avoiding substitution defined below.
Equivalence transformations on programs can be used to justify results of computations instead of directly computing with the interpreter; it is often easier. An important component of compiler optimization is applying transformations, such as the ones above, that preserve equivalence.
The variable-capture problem has appeared in the beta-equivalence above. We use renaming substitution, or capture-avoiding substitution, to deal with the problem of variable capture. Renaming substitution, e{e'/x}, is a generalized form of substitution that differs from our previously defined substitution operation e[e'/x] in that e' does not have to be closed. In such a case, we want to replace x with e', but avoid capture from occurring. This is implemented by renaming any capturing variable bindings in e. For example,
| (Function z -> (Function x -> y + x) z){x + 2/y} = |
| (Function z -> Function x1 -> x + 2 + x1) z |
Observe, in the above example, that if we had just substituted x+ 2 in for y, the x would have been “captured.” This is a bad thing, because it contradicts our definition of equivalence. We should be able to replace one equivalent thing for another anywhere, but in
Function x -> (Function z -> (Function x -> y + x) z) (x + 2)
if we ignored capture in the beta-rule we would get
Function x -> (Function z -> (Function x -> (x + 2) + x) z)
which is clearly not equivalent to the first expression. To avoid this problem, the capture-avoiding substitution operation renames x to a fresh variable not occurring in e or e', x1 in this case.
The Lambda-Calculus Now that we have defined capture-avoiding substitution, we briefly consider the lambda-calculus. In Section 2.3, we saw how to encode tuples, lists, Let statements, freezing and thawing, and even recursion in D. The encoding approach is very powerful, and also gives us a way to understand complex languages based on our understanding of simpler ones. Even numbers, booleans, and if-then-else statements are encodable, although we will skip these topics. Thus, all that is needed is functions and application to make a Turing-complete programming language. This language is known as the pure lambda calculus, because functions are usually written as lambda x.e (using the Greek “lambda” character) instead of Function x -> e.
Execution in lambda calculus is extremely straightforward and concise. The main points are as follows.
This form of computation is conceptually interesting, but is more distant from how actual computer languages execute.
It is surprisingly difficult to actually prove any of these equivalences hold. Even 1 + 1 =~ 2 is hard to prove. See [16].