3.5.2 Summary of Method
We now summarize Crofton's method for computing mean values as
follows:
There are N points independently and uniformly distributed over
some region R. One wants to calculate the mean
value of some function that depends on the relative position of
the points. Expand the space by a small increment
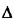 R, while preserving the same geometric shape of the
region. Now distribute the point positions uniformly and
independently over the expanded region R +
R, while preserving the same geometric shape of the
region. Now distribute the point positions uniformly and
independently over the expanded region R + 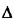 R. One can
then relate the desired mean value to the mean of the same
function, conditioned on the event that one of the points
lies within the small increment. This conditional mean value is
usually easier to calculate than is the desired mean
value. The expansion process yields a (usually) simple
first-order differential equation whose solution is the desired
mean value. It is important to note that the form of the
differential equation depends only on R, N, and the uniform
probability laws of the point positions; the solution depends on
the specific form of the function whose mean value
is desired.
R. One can
then relate the desired mean value to the mean of the same
function, conditioned on the event that one of the points
lies within the small increment. This conditional mean value is
usually easier to calculate than is the desired mean
value. The expansion process yields a (usually) simple
first-order differential equation whose solution is the desired
mean value. It is important to note that the form of the
differential equation depends only on R, N, and the uniform
probability laws of the point positions; the solution depends on
the specific form of the function whose mean value
is desired.
Problems 3.18-3.21 ask you to apply Crofton's method in certain
urban applications.
|


