Somewhere in the continuum of environments that ranges from layout-specific to system-general are a set of environments that are more detailed than are the previously described machine architectures, but that have no circuit layout associated with them. These environments specify the precise function or algorithm of a design without providing an indication of how the algorithm is realized.
The most popular algorithm-level environment is the schematic, which uses logic components to implement Boolean functions. Temporal logic is an extension of standard logic that is particularly well suited to electronic circuit specification. Another way to specify an algorithm is with a flowchart that passes either flow of control or flow of data. Of course, the most common way of specifying algorithms is with programming languages. However, textual languages can always be implemented graphically by flowcharting them. Therefore, for the purposes of this discussion, programming languages will not be considered separately from the control-flow and dataflow environments.
A schematic is a stick-figure drawing of an electronic circuit. The process of drawing a schematic is sometimes called schematic capture because it graphically represents the circuit. It is so flexible and abstract that many circuit designs start this way and are subsequently translated into some other layout-specific environment for manufacturing. Synthesis tools (described in Chapter 4) can translate a schematic into layout, producing printed circuits, integrated circuits, and more. Eventually, these tools will be able to translate reliably from higher-level input (for example system-level environments) into lower-level layout (optimized circuitry as opposed to highly regular layout). Until such time, the schematic environment will be very popular.
In digital electronic design, the schematic components are strictly
Boolean and the wires that connect these logical elements carry truth values.
For every CAD system that can do schematic design, there is
a different set of logic gates available to the designer.
In pure logic there are four operations: NOT (¬),
AND (![]() ),
OR (
),
OR (![]() ),
and IMPLICATION (
),
and IMPLICATION (![]() ),
but common practice also includes EXCLUSIVE OR (
),
but common practice also includes EXCLUSIVE OR (![]() ).
These operations are presented in a truth table in Fig. 2.6.
).
These operations are presented in a truth table in Fig. 2.6.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| FIGURE 2.6 Truth tables. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
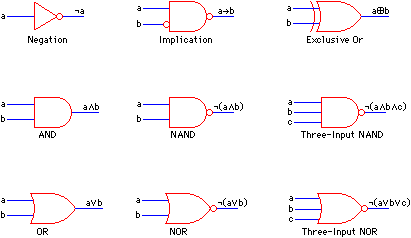
Designers often combine these functions into more complex
symbols that are treated like primitive components.
For example, NAND (![]() ) is simply the NOT of AND (the result is negated,
not the input terms).
Figure 2.7 shows some typical logic symbols and their variations.
Notice that there is only one connection in the schematic environment:
the Boolean that carries either true or false.
) is simply the NOT of AND (the result is negated,
not the input terms).
Figure 2.7 shows some typical logic symbols and their variations.
Notice that there is only one connection in the schematic environment:
the Boolean that carries either true or false.
 |
| FIGURE 2.7 Logic gates. |
In some situations, the number of different logic gates is too great and it is desirable to reduce the number of components by expressing all of them in terms of a few. For example with just one component, the NAND gate, all the previous logical operations can be derived:
| ¬ a | a | a | (a |
a | (a |
a | a |
a | (a |
These manipulations are aided by sets of equivalence rules that explain how one logic symbol can be expressed in terms of another. To prove these logical equivalences, mathematicians have developed sets of axioms. Given these axioms as truths, any logical manipulations can be done. For example, the following nine axioms are always true, regardless of the values of a, b, or c [Bell and Slomson]:
| a | (b | (a | ((a |
(¬a | (b |
(a | a | (a | b | (a | ((a |
a | (a |
b | (a |
(a | ((c |
These expressions are sufficient to define all logic because any true statement can be manipulated into one of them.
In addition to logic gates, there must be some accommodation for storage of data. Figure 1.11(b) shows the design of a flip-flop using AND, OR, NOT, and NAND gates. This circuit can be built electronically so that it correctly stores a single bit of data. With the addition of such a memory facility, any functional design can be done.
 |
| FIGURE 2.8 Military standard graphics for schematics. |
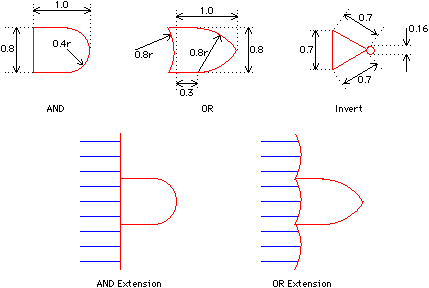
| For the builder of CAD tools, it is useful to know how to draw all these schematic elements. The U. S. government has standardized the drawing style in a document called Military Standard 806B [Department of Defense]. The standard provides proper ratios for graphics and explains how to extend symbols when there are many input lines (see Fig. 2.8). In addition, the standard provides the meaning of abbreviations (C is "clear," FF is "flip flop," RG is "register," and so on) and the proper location of annotation on bodies (top line is the function, middle line is the type of hardware, lower line is the physical location; see Fig. 2.9). Although this standard is not followed rigorously and is incomplete in some areas, it does provide a starting point for the programmer of schematics systems. |
|
Although schematics provide a good way of abstractly specifying a circuit, layout must be done at some time. To help with the conversion, there are a number of design environments that have the feel of schematics yet are much closer to layout. These environments are typically specific about some aspect of layout while abstract about the rest.
| The sticks environment is specific about the relative placement of components but abstract about their size and exact dimensions [Williams]. Transistors are drawn as stick figures with connecting wires that have no dimension (see Fig. 2.10). This design is much more specific than a schematic because abstract logic gates are not allowed. Rather, only those components that can be implemented directly in silicon are present. To convert this environment into actual layout, the components are expanded to their proper size, wires are given actual silicon layers, and the distances are adjusted to be design-rule correct. Sticks environments must be tailored to a particular type of layout. Although most are for MOS layout, there are some for bipolar design [Szabo, Leask and Elmasry]. |
|
| Another abstract environment used to approach layout is virtual grid [Weste]. As with sticks, only those components that will appear in the final layout may be used. Virtual grid, however, draws all components with a nominal size that, although not true to the final dimensions, do impart a feeling for the geometry (see Fig. 2.11). Another important feature of virtual grid design is that the relative spacings are preserved when true layout is produced. Thus two transistors that line up horizontally or vertically will stay in line, even if they are not connected. This is because the conversion to layout is simply a process that assigns actual coordinates to the virtual grid coordinates. This makes conversion quite simple yet retains the abstract nature of the design environment. |
|
Yet another pseudolayout environment is SLIC [Gibson and Nance], which describes layout component placement using text letters. An array of these letters, displayed on a video terminal, shows component placement and connecting wires. Special letters distinguish horizontal from vertical wires, and allow correct connectivity to be specified.
One problem with traditional logic is that it does not inherently deal with time in any way. One solution is to parameterize logic values with the current time, resulting in expressions like:
which means "if working at time t, and inputs are available at time t, then there will be outputs at time t + 1." However, because this structure can be awkward to use, recent work has turned to using temporal logic, a modal logic that has operators applying to sequences of states over time. Although many formulations of temporal logic have been used, this section will discuss one method that has been applied to electronic circuit descriptions [Malachi and Owicki].
Four basic operators can be used to describe state properties over time.
The symbol ![]() means "eventually" and its use in the expression
"
means "eventually" and its use in the expression
"![]() p" means that p will be true at some future time (or
is true in the present).
The symbol
p" means that p will be true at some future time (or
is true in the present).
The symbol ![]() means "henceforth" and indicates that its operand is
true now and at all future times.
The symbol
means "henceforth" and indicates that its operand is
true now and at all future times.
The symbol ![]() means "next" and indicates that its operand will be
true in the very next moment of time.
Finally, the symbol U means "until" and is used in a two-operand
sense "p U q" to mean that p is true at all times
from now until the first instance that q is true.
means "next" and indicates that its operand will be
true in the very next moment of time.
Finally, the symbol U means "until" and is used in a two-operand
sense "p U q" to mean that p is true at all times
from now until the first instance that q is true.
As with pure logic, a set of axioms relate these operators and show how they are used to define each other. For example,
states that "henceforth" p implies that p must be true now, at the next interval, and henceforth beyond that interval. A simpler tautology of temporal logic is:
In addition to basic operators, it is common to define new operators that are derived from the original set. These new operators are better suited to circuit design because they behave in ways that are more intuitive to designers. Thus the "latched while" operator is defined as:
meaning that, when p is true, it will remain that way as long as
q remains true.
Another derived operator that is important in defining the liveness
of a system is "entails" (![]() ):
):
meaning that the truth of p demands the eventual truth of q.
Temporal logic is well suited to the description of digital circuits over time. This is because it can describe the behavior of a single component or a collection of parallel activities. In fact, some form of temporal logic can be found wherever the behavior of circuits is specified. Variations on basic temporal logic exist to improve its expressiveness. For example interval temporal logic generalizes the basic scheme so that subintervals of time can be conveniently described [Moszkowski].
Flowcharting is a general-purpose algorithm environment that is often used to represent textual languages graphically. Typically, the components of a flowchart operate on data and the connections in a flowchart indicate flow of control. Each component in a flowchart can be arbitrarily complex because it contains an English-language description of its operation. Typically, however, there are a limited set of components that perform distinct classes of operations.
Figure 2.12 shows the four basic primitives that are most often used to do control-based flowcharting. The computation component is used for all data manipulations, with the actual function written in the box. The decision component is used to make arbitrary tests and modify the flow of control. The I/O component indicates control of devices. The connector component is used for special control flow cases such as are necessary in multipage designs or for program termination. The layout in Fig. 2.17 (shown later in this chapter) is an example of a control-based flowchart specification, but it does not differentiate the component types because it is a different environment (register transfer).
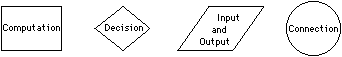 |
| FIGURE 2.12 Control-flow components. |
A somewhat different style of control-flow specification is the use of state diagrams. The components of a state diagram perform actions that may alter a global state. The connections between components are each labeled with a state, such that only one connection will match and direct the control to another component. State diagrams are a very formal way of expressing an algorithm, as opposed to flowcharting, which has imprecise rules for actions and tests.
Dataflow programming is a twist on the commonly used flowcharting technique because the connections between components carry data values rather than control invocation [Rodriguez]. This means that parallel activity is easier to specify and that the operation of an algorithm is driven by the presence of data rather than a "start" signal.
| The components of a dataflow program are called actors [Dennis] and there are many possible sets that can be used. Figure 2.13 shows one typical set of dataflow actors [Davis and Drongowski]. Dataflow actors function only when a predetermined set of input lines have data values waiting on them. This set of inputs is called the firing set. When the firing set becomes available, the actor executes and produces output values for other actors. A dataflow network that guarantees no more than one data value will be pending on any input line is safe [Patil]. |
|
The seven actors outlined in the following paragraphs are sufficient to describe any computation. In fact, some of them are redundant and exist purely for convenience.
The initiation of parallel computation is done simply by having one actor's output go to the input of multiple other actors. Then all the actors that receive input data begin operation, creating parallel execution sequences. Synchronization of these parallel paths is done with the "synch" actor that waits for all of its inputs to have data and then passes each input value to an output value at the same time. Therefore this actor synchronizes parallel data paths that complete at different times.
The "operator" actor is a general-purpose function primitive that can perform any arithmetic or logical operation. When the operation name is placed inside the actor symbol and the correct number of inputs and outputs are used, the operator functions in the proper manner. For example, the "+" actor with three inputs and one output will wait for all three data values to be present and then produce their sum on the output.
The "procedure" actor is similar to the "operator" actor except that it is used for programmer-defined functions. The name of a dataflow subroutine is placed inside the symbol as an indication that this code is to be run when the appropriate inputs appear. Both this actor and the "operator" actor are subroutine calls, but the former is for higher-level procedures whereas the latter is for low-level library functions.
The "distribute" actor is used to select among multiple output paths according to an index value. When the input and the index lines have data, this actor sends the input value to the output line specified by the index value. This actor is somewhat like a "case" statement in traditional programming languages and is also used for simpler "if"-type branching.
The "select" and "arbiter" actors are conceptually the opposite of "distribute" because they reduce multiple input values to a single output value in a controlled manner. In the case of the "select" actor, an index is used to determine which input will be used. When the index and the indexed input are present, that input is passed to the output. The "arbiter" does not need any particular input; rather, it executes as soon as any input appears, generating both the input and its index as outputs. Both "select" and "arbiter" reduce many inputs to a single output: One requires a predetermined choice of inputs and the other reports its own choice.
The final actor of this particular dataflow environment is the "gate," which is used for loop control. This actor has three inputs and an output. The condition input acts as a switch to select between the initial input and the feedback input. When the loop is not active, the condition is false, which causes the initial value to be passed to the output. Once this initial value is passed to the output, the loop is activated. Active "gate" actors ignore the initial value and pass the feedback value to the output. This continues while the condition input is true. When this condition becomes false, the loop terminates, the feedback values are ignored, and a new initial value is awaited to restart the loop.
| The dataflow actors described here can be used to write arbitrarily complex algorithms. The design in Fig. 2.14 shows the computation of Fibonacci numbers in a recursive and parallel style. Notice that this subroutine starts at the bottom with its input parameters and filters up to the top where the function value is returned. This layout uses only the "operator," "procedure," "select," and "distribute" actors and thus does not make use of the powerful concurrency control available in the environment. Nevertheless, graphically specified dataflow is a useful environment for the design of algorithms, both serial and parallel. |
|
| Previous | Table of Contents | Next | Static Free Software |