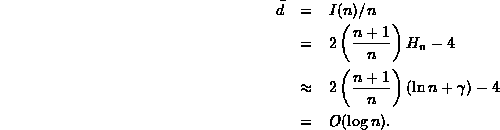This section presents a technique for solving recurrence relations
such as Equation ![]() called telescoping .
The basic idea is this:
We rewrite the recurrence formula so that a similar functional
form appears on both sides of the equal sign.
E.g., in this case, we consider n>2 and divide
both sides of Equation
called telescoping .
The basic idea is this:
We rewrite the recurrence formula so that a similar functional
form appears on both sides of the equal sign.
E.g., in this case, we consider n>2 and divide
both sides of Equation ![]() by n+1 to get
by n+1 to get
![]()
Since this equation is valid for any n>2, we can write the following series of equations:
Each subsequent equation in this series is obtained by substituting n-1 for n in the preceding equation. In principle, we repeat this substitution until we get an expression on the right-hand-side involving the base case. In this example, we stop at n-k-1=2.
Because Equation ![]() has a similar functional form on both
sides of the equal sign,
when we add Equation
has a similar functional form on both
sides of the equal sign,
when we add Equation ![]() through Equation
through Equation ![]() together,
most of the terms cancel leaving
together,
most of the terms cancel leaving
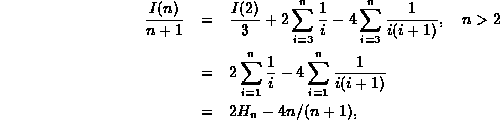
where ![]() is the
is the ![]() harmonic number .
In Section
harmonic number .
In Section ![]() it is shown that
it is shown that
![]() ,
where
,
where ![]() is called Euler's constant .
Thus, we get that the average internal path length of the average
binary search tree with n internal nodes is
is called Euler's constant .
Thus, we get that the average internal path length of the average
binary search tree with n internal nodes is
![]()
Finally, we get to the point: The average depth of a node in the average binary search tree with n nodes is