Unsuccessful Search

All successful searches terminate when the object of the search is found. Therefore, all successful searches terminate at an internal node. In contrast, all unsuccessful searches terminate at an external node. In terms of the binary tree shown in Figure , a successful search terminates in one of the nodes which are drawn as a circles and an unsuccessful search terminates in one of the boxes.

The preceding analysis shows that the average number of nodes visited during a successful search depends on the internal path length  , which is simply the sum of the depths of all the internal nodes. Similarly, the average number of nodes visited during an unsuccessful search depends on the external path length  , which is the sum of the depths of all the external nodes. Fortunately, there is a simple relationship between the internal path length and the external path length of a binary tree.

Theorem  Consider a binary tree T with n internal nodes and an internal path length of I. The external path length of T is given by

In other words, Theorem  says that the difference between the internal path length and the external path length of a binary tree with n internal nodes is E-I=2n.

extbfProof (By induction).

Base Case Consider a binary tree with one internal node and internal path length of zero. Such a tree has exactly two empty subtrees immediately below the root and its external path length is two. Therefore, the theorem holds for n=1.

Inductive Hypothesis Assume that the theorem holds for for some . Consider an arbitrary tree, , that has k internal nodes. According to Theorem , has k+1 external nodes. Let and be the internal and external path length of , respectively, According to the inductive hypothesis, .

Consider what happens when we create a new tree by removing an external node from and replacing it with an internal node that has two empty subtrees. Clearly, the resulting tree has k+1 internal nodes. Furthermore, suppose the external node we remove is at depth d. Then the internal path length of is and the external path length of is .

The difference between the internal path length and the external path length of is

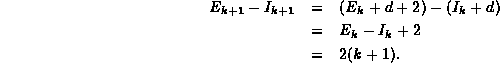
Therefore, by induction on k, the difference between the internal path length and the external path length of a binary tree with n internal nodes is 2n for all .

Since the difference between the internal and external path lengths of any tree with n internal nodes is 2n, then we can say the same thing about the average internal and external path lengths averaged over all search trees. Therefore, E(n), the average external path length of a binary search tree is given by

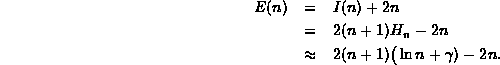
A binary search tree with internal n nodes has n+1 external nodes. Thus, the average depth of an external node of a binary search tree with n internal nodes, , is given by

These very nice results are the raison d'être for binary search trees. What they say is that the average number of nodes visited during either a successful or an unsuccessful search in the average binary search tree having n nodes is . We must remember, however, that these results are premised on the assumption that all possible search trees of n nodes are equiprobable. It is important to be aware that in practice this may not always be the case.

Copyright © 1997 by Bruno R. Preiss, P.Eng. All rights reserved.