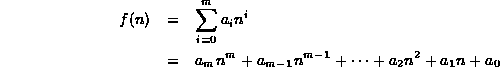
where ![]() .
Then
.
Then ![]() .
.
In this section we examine the asymptotic behavior of polynomials in n. In particular, we will see that as n gets large, the term involving the highest power of n will dominate all the others. Therefore, the asymptotic behavior is determined by that term.
Theorem Consider a polynomial in n of the form
where
. Then
.
extbfProof
Each of the terms in the summation is of the form ![]() .
Since n is non-negative,
a particular term will be negative only if
.
Since n is non-negative,
a particular term will be negative only if ![]() .
Hence, for each term in the summation,
.
Hence, for each term in the summation, ![]() .
Recall too that we have stipulated that the coefficient of the
largest power of n is positive, i.e.,
.
Recall too that we have stipulated that the coefficient of the
largest power of n is positive, i.e., ![]() .
.
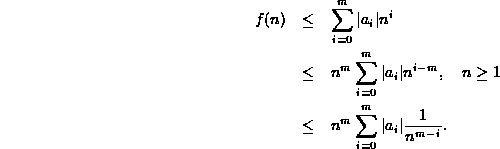
Note that for integers ![]() ,
,
![]() for
for ![]() . Thus
. Thus
From Equation ![]() we see that
we have found the constants
we see that
we have found the constants ![]() and
and ![]() ,
such that for all
,
such that for all ![]() ,
, ![]() .
Thus,
.
Thus, ![]() .
.
This property of the asymptotic behavior of polynomials
is used extensively.
In fact, whenever we have a function,
which is a polynomial in n,
![]() we will immediately ``drop'' the less significant terms
(i.e., terms involving powers of n which are less than m),
as well as the leading coefficient,
we will immediately ``drop'' the less significant terms
(i.e., terms involving powers of n which are less than m),
as well as the leading coefficient, ![]() ,
to write
,
to write ![]() .
.