In this section we determine the asymptotic behavior of logarithms.
Interestingly,
despite the fact that ![]() diverges as n gets large,
diverges as n gets large,
![]() for all integers
for all integers ![]() . Hence,
. Hence, ![]() .
Furthermore, as the following theorem will show,
.
Furthermore, as the following theorem will show,
![]() raised to any integer power
raised to any integer power ![]() is still O(n).
is still O(n).
Theorem For every integer,
.
extbfProof
This result follows immediately from Theorem ![]() and the observation that for all integers
and the observation that for all integers ![]() ,
,
This observation can be proved by induction as follows:
Base Case Consider the limit
![]()
for the case k=1.
Using L'Hôpital's rule![]() we see that
we see that

Inductive Hypothesis
Assume that Equation ![]() holds for
holds for ![]() .
Consider the case k=m+1.
Using L'Hôpital's rule we see that
.
Consider the case k=m+1.
Using L'Hôpital's rule we see that
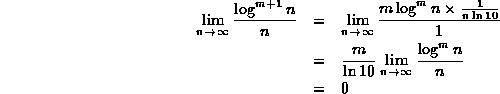
Therefore, by induction on m, Equation ![]() holds for all integers
holds for all integers ![]() .
.
For example,
using this property of logarithms
together with the rule for determining the asymptotic behavior
of the product of two functions (Theorem ![]() ),
we can determine that since
),
we can determine that since ![]() ,
then
,
then ![]() .
.