Comparison of Modules and Objects
The main difference between modular programming and object
programming in Objective CAML comes from the type system.
In effect, programming with modules remains within
the ML type system (i.e. parametric polymorphism code is
executed for different types of parameter), while programming with
objects entails an ad hoc polymorphism (in which the sending of
a message to an object triggers the application of different pieces of
code). This is particularly clear with subtyping. This extension of
the ML type system can not be simulated in pure ML. It will
always be impossible to construct heterogeneous lists without breaking
the type system.
Modular programming and object programming are two safe (thanks to
typing) approaches to the logical organisation of a program,
permitting the reusability and the modifiability of software
components. Programming with objects in Objective CAML allows parametric
polymorphism (parameterized classes) and inclusion/subtype
polymorphism (sending of messages) thanks to late binding and
subtyping, with restrictions due to equality, facilitating
incremental programming. Modular programming allows one to restrict
parametric polymorphism and use immediate binding, which can be useful
for conserving efficiency of execution.
The modular programming model permits the easy extension of functions
on non-extensible recursive data types. If one wishes to add a case in
a variant type, it will be necessary to modify a large part of the
sources.
The object model of programming defines a set of recursive
data types using classes. One interprets a class as a case of the
data type.
Efficiency of Execution
Late binding corresponds to an indirection in the method table (see page
??). Just as the access to an instance variable from
outside the class goes through a message dispatch, this
accumulation of indirections can prove to be costly.
To show this loss of efficiency, we construct the following class hierarchy:
# class virtual test () =
object
method virtual sum : unit -> int
method virtual sum2 : unit -> int
end;;
# class a x =
object(self)
inherit test ()
val a = x
method a = a
method sum () = a
method sum2 () = self#a
end;;
# class b x y =
object(self)
inherit a x as super
val b = y
method b = b
method sum () = b + a
method sum2 () = self#b + super#sum2()
end;;
Now, we compare the execution time, on one hand of the dispatch of
messages sum and sum2 to an instance of class
b, and on the other hand of a call to the following function
f.
# let f a b = a + b ;;
# let iter g a n = for i = 1 to n do ignore(g a) done ; g a ;;
# let go i j = match i with
1 -> iter (fun x -> x#sum()) (new b 1 2) j
| 2 -> iter (fun x -> x#sum2()) (new b 1 2) j
| 3 -> iter (fun x -> f 1 x) 2 j ;;
# go (int_of_string (Sys.argv.(1))) (int_of_string (Sys.argv.(2))) ;;
For 10 million iterations, we get the following results:
| |
bytecode |
native |
| case 1 |
07,5 s |
0,6 s |
| case 2 |
15,0 s |
2,3 s |
| case 3 |
06,0 s |
0,3 s |
This example has been constructed in order to show that late
binding has a cost relative to the standard static binding. This cost
depends on the quantity of calculation relative to the number of
message dispatches in a function. The use of the native compiler
reduces the calculation component without changing the indirection
component of the test. We can see in case 2 that
the multiple indirections at the dispatch of message
sum2 have an ``incompressible'' cost.
Example: Graphical Interface
The AWI graphical library (see page ??) was
designed using the functional/imperative core of the language. It is
very easy to adapt it into module form. Each component becomes an
independent module, thus permitting a harmonization of function names.
To add a component, it is necessary to know the concrete type of its
components. It is up to the new module to modify the fields necessary
to describe its appearance and its behaviors.
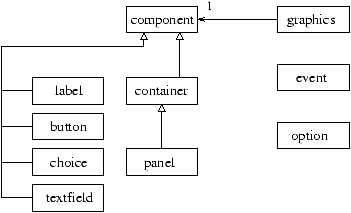
The library can also be rewritten as an object. For this we construct the
hierarchy of classes shown in figure 16.1.
Figure 16.1: Class hierarchy for AWI.
It is easier to add new components, thanks to inheritance, than when
using modules; however, the absence of overloading still requires
options to be encoded as method parameters. The use of
the subtyping relation makes it easy to construct a list of
the constituents of a container. Deferred linking selects
the methods appropriate to the component. The interest
of the object model also comes from the possibility of extending or
modifying the graphics context, and the other types that are used,
again thanks to inheritance. This is why the principal
graphics libraries are organised according to the object model.
Translation of Modules into Classes
A simple module which only declares one type and does not have any
type-independent polymorphic functions can be translated into a
class. According to the nature of the type used (record type or
variant type) one translates the module into a class in a different
way.
Type Declarations
Record type.
A record type can be written directly in the form of a class
in which every field of the record type becomes an instance variable.
Variant type.
A variant type translates into many classes, using the conceptual
model of a ``composite''. An abstract class describes the operations
(functions) on this type. Every branch of the variant type thus
becomes a subclass of the abstract class, and implements the abstract
methods for its branch. We no longer have pattern
matching but instead choose the method specific to the branch.
Parameterized types.
Parameterized types are implemented by parameterized classes.
Abstract types.
We can consider a class as an abstract type. At no time is the
internal state of the class visible outside its hierarchy.
Nevertheless, nothing prevents us from defining a subclass in
order to access the variables of the instances of a class.
Mutually recursive types.
The declarations of mutually recursive types are translated into
declarations of mutually recursive classes.
Function Declarations
Those functions with parameters dependent on the module type,
t, are translatable into methods. Functions in which
t does not appear may be declared private inasmuch as
their membership of the module is not directly linked to the type
t. This has the added advantage that there is no
problem if type variables appear in the type of the parameters. We
are left with the problem of functions in which one parameter is of
type t and another is of type 'a. These functions
are very rare in the modules of the standard library. We can identify
``peculiar'' modules like Marshal or Printf which
have non-standard typing, and modules (that operate) on linear
structures like List. For this last, the function
fold_left, of type ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a is
difficult to translate, especially in a method of the class
['b] list because the type variable 'a is free and
may not appear in the type of the method. Rather than adding a type
parameter to the list class, it is preferable to break these
functions out into new classes, parameterized by two type variables
and having a list field.
Binary methods.
Binary methods do not pose any problem, outside subtyping.
Other declarations.
Declarations of non-functional values. We can accept the declaration
of non-functional values outside classes. This is also true for
exceptions.
Example: Lists with Iterator.
We are trying to translate a module with the following signature LIST
into an object.
# module type LIST = sig
type 'a list = C0 | C1 of 'a * 'a list
val add : 'a list -> 'a -> 'a list
val length : 'a list -> int
val hd : 'a list -> 'a
val tl : 'a list -> 'a list
val append : 'a list -> 'a list -> 'a list
val fold_left : ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a
end ;;
First of all, we declare the abstract class 'a list corresponding to
the definition of the type.
# class virtual ['a] list () =
object (self : 'b)
method virtual add : 'a -> 'a list
method virtual empty : unit -> bool
method virtual hd : 'a
method virtual tl : 'a list
method virtual length : unit -> int
method virtual append : 'a list -> 'a list
end ;;
Then we define the two subclasses c1_list and
c0_list for each constituent of the variant type. Each of
these classes should define the methods of the ancestor abstract class
# class ['a] c1_list (t, q) =
object (self )
inherit ['a] list () as super
val t = t
val q = q
method add x = new c1_list (x, (self : 'a #list :> 'a list))
method empty () = false
method length () = 1 + q#length()
method hd = t
method tl = q
method append l = new c1_list (t,q#append l)
end ;;
# class ['a] c0_list () =
object (self)
inherit ['a] list () as super
method add x = new c1_list (x, (self : 'a #list :> 'a list))
method empty () = true
method length () = 0
method hd = failwith "c0_list : hd"
method tl = failwith "c0_list : tl"
method append l = l
end ;;
# let l = new c1_list (4, new c1_list (7, new c0_list ())) ;;
val l : int list = <obj>
The function LIST.fold_left has not been incorporated into
the list class to avoid introducing a new type parameter.
We prefer to define the class fold_left to implement this
method. For this, we use a functional instance variable
(f).
# class virtual ['a,'b] fold_left () =
object(self)
method virtual f : 'a -> 'b -> 'a
method iter r (l : 'b list) =
if l#empty() then r else self#iter (self#f r (l#hd)) (l#tl)
end ;;
# class ['a,'b] gen_fl f =
object
inherit ['a,'b] fold_left ()
method f = f
end ;;
Thus we construct an instance of the class gen_fl for addition:
# let afl = new gen_fl (+) ;;
val afl : (int, int) gen_fl = <obj>
# afl#iter 0 l ;;
- : int = 11
Simulation of Inheritance with Modules
Thanks to the relation of inheritance between classes,
we can retrieve in a subclass the collection of variable
declarations and methods of the ancestor class.
We can simulate this relation by
using modules. The subclass which inherits is transformed into a
parameterized module, of which the parameter is the ancestor class.
Multiple inheritance increases the number of parameters of
the module. We revisit the classic example of points and colored
points, described in chapter 15, to translate it into
modules.
The class point becomes the module Point with the
following signature POINT.
# module type POINT =
sig
type point
val new_point : (int * int) -> point
val get_x : point -> int
val get_y : point -> int
val moveto : point -> (int * int) -> unit
val rmoveto : point -> (int * int) -> unit
val display : point -> unit
val distance : point -> float
end ;;
The class colored_point is transformed into a parameterized module ColoredPoint
which has the signature POINT as its parameter.
# module ColoredPoint = functor (P : POINT) ->
struct
type colored_point = {p:P.point;c:string}
let new_colored_point p c = {p=P.new_point p;c=c}
let get_c self = self.c
(* begin *)
let get_x self = let super = self.p in P.get_x super
let get_y self = let super = self.p in P.get_y super
let moveto self = let super = self.p in P.moveto super
let rmoveto self = let super = self.p in P.rmoveto super
let display self = let super = self.p in P.display super
let distance self = let super = self.p in P.distance super
(* end *)
let display self =
let super = self.p in P.display super; print_string ("has color "^ self.c)
end ;;
The burden of ``inherited'' declarations can be lightened by an
automatic translation procedure, or an extension of the language.
Recursive method declarations can be written with a single
let rec ... and. Multiple inheritance leads to functors with many
parameters. The cost of redefinition is not greater than that of late
binding.
Late binding is not implemented in this simulation. To achieve it, it
is necessary to define a record in which each field corresponds to the
type of its functions/methods.
Limitations of each Model
The functional/modular module offers a reassuring but rigid framework
for the modifiability of code. Objective CAML's object model suffers from
``double vision'' of classes: structuring and type, implying the
absence of overloading and the impossibility of imposing type
constraints from an ancestor type on a descendant type.
Modules
The principal limitations of the functional/modular model arise from
the difficulty of extending types. Although abstract types
allow us to get away from the concrete representation of
a type, their use in parameterized modules requires that type
equalities between modules be indicated by hand,
complicating the writing of signatures.
Recursive dependencies.
The dependence graph of the modules in an application is a
directed acyclic graph (DAG). This implies on the one hand that there
are no types that are mutually recursive between two modules, and on
the other prevents the declaration of mutually recursive values.
Difficulties in writing signatures.
One of the attractions of type inference is that it is not necessary
to specify the types of function parameters. The specification of
signatures sacrifices this convenience. It becomes necessary to
specify the types of the declarations of the signature ``by hand.''
One can use the -i option of the compiler ocamlc to
display the type of all the global declarations in a .ml file
and use this information to construct the signature of a module. In
this case, we lose the ``software engineering'' discipline which
consists of specifying the module before implementing it. In
addition, if the signature and module undergo large changes, we will
have to go back to editing the signature. Parameterized modules need
signatures for their parameters and those should also be written by
hand. Finally if we associate a functional signature with a
parameterized module, it is impossible to recove the
signature resulting from the application of the functor. This obliges
us to mostly write non-functional signatures, leaving it until
later to assemble them to construct a functional signature.
Import and export of modules.
The importation of the declarations of a simple module is achieved
either by dot notation (Module.name) or directory by the name
of a declaration (name) if the model has been opened
(open Module). The declaration of the interface of
the imported module is not directly exportable at the level of the
module in process of being defined. It has access to these
declarations, but they are not considered as declarations of the
module. In order to do this it is necessary to declare, in the same
way as the simulation of inheritance, imported values. The same is
true for parameterized modules. The declarations of the module
parameters are not considered as declarations of the current module.
Objects
The principle limitations of the Objective CAML object model arise from typing.
-
no methods containing parameters of free type;
- difficulty of escaping from the type of a class in one of its methods;
- absence of type constraint from the ancestor type on its descendant;
- no overloading;
The most disconcerting point when you start with the object
extension of Objective CAML is the impossibility of constructing methods
containing a parameterized type in which the type parameter is
free. The declaration of a class can be seen as the definition of a new
type, and hence arises the general rule forbidding the presence of variables
with free type in the declaration of a type.
For this reason, parameterized classes are
indispensable in the Objective CAML object model because they permit the
linking of their type variables.
Absence of overloading.
The Objective CAML object model does not allow method overloading. As the
type of an object corresponds to types of its methods, the fact of
possessing many methods with the same name but different types would
result in numerous ambiguities, due to parametric polymorphism, which
the system could only resolve dynamically. This would be
contradictory to the vision of totally static typing. We
take a class example which has two message methods, the first
having an integer parameter, and the second a float parameter. Let
e be an instance of this class and f be the
following function:
# let f x a = x#message a ;;
The calls f e 1 et f e 1.1 cannot be statically
resolved because there is no information about the class
example in the code of the function f.
An immediate consequence of this absence is the uniqueness of instance
constructors. The declaration of a class indicates the parameters to
supply to the creation function. This constructor is unique.
Initialization.
The initialization of instance variables declared in a class can be
problematic when it should be calculated based on the values passed to
the constructor.
Equality between instances.
The only equality which applies to objects is physical equality.
Structural equality always returns false when it is applied
to two physically different objects. This can be surprising inasmuch
as two instances of the same class share the same method table. One
can imagine a physical test on the method table and a structural test
on the values (val) of objects. These are the implementation
choices of the linear pattern-matching style.
Class hierarchy.
There is no class hierarchy in the language distribution. In
fact the collection of libraries are supplied in the form of
simple or parameterized modules. This demonstrates that the object
extension of the language is still stabilizing,
and makes little case for its extensive use.