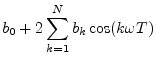Example Zero-Phase Filters

A practical zero phase filter was illustrated in Figures 11.1 and 11.2. In this section, we look further at some simpler cases.

The trivial (non-) filter $h(n)=\delta(n)$ has frequency response $H(e^{j\omega T})=1$, which is truly zero phase,

Every second-order zero-phase FIR filter has an impulse response of the form

$$h(n) = b_{1}\delta(n+1) + b_0\delta(n) + b_1 \delta(n-1).$$

The transfer function of such a filter is

$$H(z) = b_{1}z + b_0 + b_1 z^{-1}$$

and the frequency response is

$$H(e^{j\omega T}) = b_{1}e^{j\omega T}+ b_0 + b_1 e^{-j\omega T}= b_0 + 2 b_1 \cos(\omega T)$$

which is real for all $\omega$. The dc response is $H(1) = b_0 + 2 b_1$, which is positive (truly zero phase) provided $b_0>-2b_1$, while the $f_s/2$ response is $H(-1) = b_0 - 2 b_1$ which may be either positive or negative.

Extending the previous example, every order $2N+1$ zero-phase FIR filter has an impulse response of the form

$$h(n) = b_{N}\delta(n+N) + \cdots + b_{1}\delta(n+1) + b_0\delta(n) + b_1 \delta(n-1) + \cdots b_N\delta(n-N)$$

and frequency response

$$b_0 + 2 \sum_{k=1}^N b_k \cos(k\omega T)$$

which is clearly real whenever the coefficients $b_k$ are real.