Zero-Phase Filters
(Even Impulse Responses)

A zero-phase filter is a special case of a linear-phase filter in which the phase slope is $\alpha=0$. The real impulse response $h(n)$ of a zero-phase filter is even.^12.1That is, it satisfies

$$h(n) = h(-n). \qquad\hbox{(Zero-Phase Condition)}$$

Note that every even signal is symmetric, but not every symmetric signal is even. To be even, it must be symmetric about time 0.

Note that a zero-phase filter cannot be causal (except in the trivial case when the filter is a constant scale factor $h(n)=g\delta(n)$). However, in many ``off-line'' applications, such as when filtering a sound file on a computer disk, causality is not a requirement, and zero-phase filters are usually preferred.

It is a well known Fourier symmetry that real, even signals have real, even Fourier transforms. Therefore,

$\parbox{0.8\textwidth}{\emph{a real, even impulse response corresponds to a real, \\ even frequency response.}}$

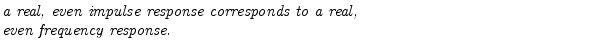
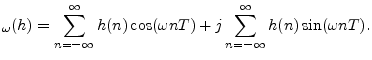
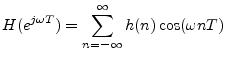
This follows immediately from writing the DTFT of $h$ in terms of a cosine and sine transform,

$$H(e^{j\omega T}) =$$   DTFT$$_\omega(h) = \sum_{n=-\infty}^\infty h(n) \cos(\omega nT) + j \sum_{n=-\infty}^\infty h(n) \sin(\omega nT).$$

Since $h$ is even, cosine is even, and sine is odd; and since even times even is even, and even times odd is odd; and since the sum over an odd function is zero, we have that

$$H(e^{j\omega T}) = \sum_{n=-\infty}^\infty h(n) \cos(\omega nT)$$

for a zero-phase filter $h$. This is a real and even function of $\omega$.

A real frequency response has phase zero when it is positive, and a phase of $\pi$ radians when it is negative. Therefore, a ``zero-phase filter,'' as we have defined [ $h(n) = h(-n)$] may actually have a phase response of 0 or $\pi$ at each frequency. In practice, the filter is usually precisely zero-phase in all ``pass bands'', while it switches between 0 and $\pi$ in the stop bands (frequency intervals where the gain is desired to be zero). A better name, in general, would be piecewise constant-phase filter. For any real filter, the constant phase can be either 0 or $\pi$. Similarly, the term ``linear phase'' could be sharpened to ``linear-phase with discontinuities by any multiple of $\pi$ radians''.

Figure 11.1: Impulse response and frequency response of a length 11 zero-phase FIR lowpass filter. Note that the frequency response is real because the filter is zero phase. Also plotted (in dashed lines) are the requested pass-band and stop-band gains.

Figure 11.1 shows the impulse response and frequency response of a length 11 zero-phase FIR lowpass filter designed using the Remez exchange algorithm.^12.2 The Matlab code for designing this filter is as follows:

N = 11;                % filter length - must be odd
b = [0 0.1 0.2 0.5]*2; % band edges
M = [1  1   0   0 ];   % desired band values
h = remez(N-1,b,M);    % Remez multiple exchange design

The impulse response h is returned in linear-phase form, so it must be left-shifted $(N-1)/2=5$ samples to make it zero phase.

Figure 11.2: Amplitude response and phase response of the length 11 zero-phase FIR lowpass filter.

Figure 11.2 shows the amplitude and phase responses of the FIR filter. We see that each zero-crossing in the frequency response results in a phase jump of $\pi$ radians. The phase is zero throughout the pass-band, but in the stop-band, the phase alternates between zero and $\pi$. In practice, very few ``zero-phase filters'' have a truly zero phase response at all frequencies. Instead, the phase typically alternates between zero and $\pi$, as shown in Fig.11.2. However, the $\pi$ phase values typically occur only in the stop-band of the filter, i.e., at frequencies where the amplitude response is so small that it can be neglected. At frequencies for which the phase response is $\pi$, the filter may be said to be ``inverting'', i.e., it negates the frequency components at such frequencies.

In view of the foregoing, the term ``zero-phase filter'' is only approximately descriptive. More precise terms would be 0-or-$\pi$-phase filter, even-impulse-response filter, or real-frequency-response filter.