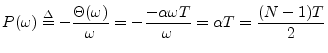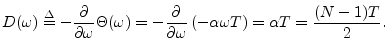Filters Preserving Phase

In this chapter, linear phase and zero phase filters are defined and discussed.

When one wishes to modify only a signal's magnitude-spectrum and not its spectral phase, then a linear-phase filter is desirable. (The name linear-phase-response filter would be more precise.) Linear-phase filters have a symmetric impulse response, i.e.,

$$h(n) = h(N-1-n) \qquad\hbox{(Linear-Phase Condition)}$$

for $n=0,1,2,\ldots,N-1$, where $h(n)$ is the length $N$ impulse response of a causal FIR filter. Causal recursive filters cannot have symmetric impulse responses.

We will show that every symmetric impulse response corresponds to a real frequency response times a linear phase term $e^{-j\alpha\omega T}$, where $\alpha = (N-1)/2$ is the slope of the linear phase. Linear phase is often ideal because a filter phase of the form $\Theta(\omega) = - \alpha \omega T$ corresponds to phase delay

$$P(\omega) \isdef - \frac{\Theta(\omega)}{\omega} = - \frac{-\alpha\omega T}{\omega} = \alpha T = \frac{(N-1)T}{2}$$

and group delay

$$D(\omega) \isdef - \frac{\partial}{\partial \omega}\Theta(\omega... ...l}{\partial \omega}\left(-\alpha\omega T\right) = \alpha T = \frac{(N-1)T}{2}.$$

That is, both the phase and group delay of a linear-phase filter are equal to $(N-1)/2$ samples of plain delay at every frequency. Since a length $N$ FIR filter implements $N-1$ samples of delay, the value $(N-1)/2$ is exactly half the total filter delay. Delaying all frequency components by the same amount preserves the waveshape as much as possible for a given amplitude response.