Matlab Filter Implementation

In this section, we will implement (in matlab) the simplest lowpass filter

$$y(n) = x(n) + x(n-1),\;n=1,2,\ldots,N$$

(from Eq. (1.1)). This implementation will work with minor modifications for any causal digital filter in so-called ``direct form.''^3.3

For the simplest lowpass filter, we had two program listings:

• Fig.1.3 listed simplp for filtering one block of data, and
• Fig.1.4 listed a main program for testing simplp.

In matlab, there is a built-in function called filter^3.4 which will implement simplp as a special case. The syntax is

        y = filter (B, A, x)

where

x is the input signal (a vector of any length),

y is the output signal (returned equal in length to x),

A is a vector of filter feedback coefficients, and

B is a vector of filter feedforward coefficients.

The filter routine performs the following iteration over the elements of x to implement any causal, finite-order, linear, time-invariant digital filter:

$$\texttt{y}(n) = \sum_{k=0}^{M_n} \texttt{B}(k+1) \texttt{x}(n-k)$$

$$- \sum_{k=1}^{N_n} \texttt{A}(k+1) \texttt{y}(n-k), \quad n=1,2,\ldots,N_x \protect$$ (3.1)

where $N_x \isdef \texttt{length(x)}$, $N_n\isdef \min\{N,n-1\}$, $M_n\isdef \min\{M,n-1\}$, $M+1$ is the length of B, $N+1$ is the length of A, and $\texttt{A}(1)$ is assumed to be 1. (Otherwise, B and A are divided through by A(1). Note that A(1) is not used in Eq. (2.1).) The relatively awkward indexing in Eq. (2.1) is due to the fact that, in matlab, all array indices start at 1, not 0 as in most C programs.

Note that Eq. (2.1) could be written directly in matlab using two for loops (as shown in Fig.3.2). However, this would execute much slower because the matlab language is interpreted, while built-in routines such as filter are pre-compiled C modules. As a general rule, matlab programs should avoid iterating over individual samples whenever possible. Instead, whole signal vectors should be processed using expressions involving vectors and matrices. In other words, algorithms should be ``vectorized'' as much as possible. Accordingly, to get the most out of matlab, it is necessary to know some linear algebra [58].

The simplest lowpass filter of Eq. (1.1) is nonrecursive (no feedback), so the feedback coefficient vector A is set to 1.^3.5 (Recursive filters will be introduced later in §5.1.) The minus sign in Eq. (2.1) will make sense after we look at filter transfer functions in Chapter 6.

The feedforward coefficients needed for the simplest lowpass filter are

$$\texttt{B}= [ 1 , 1 ],$$

With these settings, the filter function implements

$$\begin{eqnarray*} \texttt{y}(1) &=& \texttt{B}(1) \cdot \texttt{x}(1)\\ \texttt... ...texttt{x}(n-1), \qquad n=2,3,\ldots,\texttt{length}(\texttt{x}). \end{eqnarray*}$$

Figure 2.1: Main matlab program for implementing the simplest low-pass filter $y(n) = x(n) + x(n - 1)$.

 

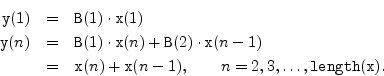
% simplpm1.m - matlab main program implementing 
%              the simplest lowpass filter:
%
%                    y(n) = x(n)+x(n-1)}

N=10;       % length of test input signal
x = 1:N;    % test input signal (integer ramp)
B = [1,1];  % feedforward coefficients
A = 1;      % feedback coefficients (none)

y = filter(B,A,x);

for i=1:N
  disp(sprintf('x(%d)=%f\ty(%d)=%f',i,x(i),i,y(i)));
end

% Output: 
%   octave:1> simplpm1
%   x(1)=1.000000       y(1)=1.000000
%   x(2)=2.000000       y(2)=3.000000
%   x(3)=3.000000       y(3)=5.000000
%   x(4)=4.000000       y(4)=7.000000
%   x(5)=5.000000       y(5)=9.000000
%   x(6)=6.000000       y(6)=11.000000
%   x(7)=7.000000       y(7)=13.000000
%   x(8)=8.000000       y(8)=15.000000
%   x(9)=9.000000       y(9)=17.000000
%   x(10)=10.000000     y(10)=19.000000

A main test program analogous to Fig.1.4 is shown in Fig.2.1. Note that the input signal is processed in one big block, rather than being broken up into two blocks as in Fig.1.4. If we want to process a large sound file block by block, we need some way to initialize the state of the filter for each block using the final state of the filter from the preceding block. The filter routine accommodates this usage with an additional optional input and output argument:

        [y, Sf] = filter (B, A, x, Si)

Si denotes the filter initial state, and Sf denotes its final state. A main program illustrating block-oriented processing is given in Fig.2.2.

Figure: Block-oriented version of the matlab program in Fig.2.1.

 

% simplpm2.m - block-oriented version of simplpm1.m

N=10;       % length of test input signal
NB=N/2;     % block length
x = 1:N;    % test input signal
B = [1,1];  % feedforward coefficients
A = 1;      % feedback coefficients (none)

[y1, Sf] = filter(B,A,x(1:NB));      % process block 1
      y2 = filter(B,A,x(NB+1:N),Sf); % process block 2

for i=1:NB   % print input and output for block 1
  disp(sprintf('x(%d)=%f\ty(%d)=%f',i,x(i),i,y1(i)));
end

for i=NB+1:N % print input and output for block 2
  disp(sprintf('x(%d)=%f\ty(%d)=%f',i,x(i),i,y2(i-NB)));
end