| (8.1) |
A reason for the importance of convolution (defined in §7.2.4) is that every linear time-invariant system8.3can be represented by a convolution. Thus, in the convolution equation
The impulse or ``unit pulse'' signal is defined by
![$\displaystyle \delta(n) \isdef \left\{\begin{array}{ll}
1, & n=0 \\ [5pt]
0, & n\neq 0. \\
\end{array}\right.
$](img1503.png)
The impulse signal is the identity element under convolution, since
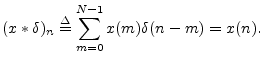
It turns out in general that every linear time-invariant (LTI) system
(filter) is completely described by its impulse response [66].
No matter
what the LTI system is, we can feed it an impulse, record what comes
out, call it ![]() , and implement the system by convolving the input
signal
, and implement the system by convolving the input
signal ![]() with the impulse response
with the impulse response ![]() . In other words, every LTI
system has a
convolution representation in terms of its impulse response.
. In other words, every LTI
system has a
convolution representation in terms of its impulse response.