It is instructive to study the modulation of one sinusoid by another. In this section, we will look at sinusoidal Amplitude Modulation (AM). The general AM formula is given by
Let's analyze the second term of Eq. (4.1) for the case of sinusoidal
AM with ![]() and
and
![]() :
:
When ![]() is small (say less than
is small (say less than ![]() radians per second, or
10 Hz), the signal
radians per second, or
10 Hz), the signal ![]() is heard as a ``beating sine wave'' with
is heard as a ``beating sine wave'' with
![]() beats per second. The beat rate is
twice the modulation frequency because both the positive and negative
peaks of the modulating sinusoid cause an ``amplitude swell'' in
beats per second. The beat rate is
twice the modulation frequency because both the positive and negative
peaks of the modulating sinusoid cause an ``amplitude swell'' in
![]() . (One period of modulation--
. (One period of modulation--![]() seconds--is shown in
Fig.4.11.) The sign inversion during the negative peaks is not
normally audible.
seconds--is shown in
Fig.4.11.) The sign inversion during the negative peaks is not
normally audible.
Recall the trigonometric identity for a sum of angles:
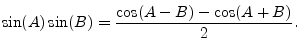
Equation (4.3) expresses ![]() as a ``beating sinusoid'', while
Eq. (4.4) expresses as it two unmodulated sinusoids at
frequencies
as a ``beating sinusoid'', while
Eq. (4.4) expresses as it two unmodulated sinusoids at
frequencies
![]() . Which case do we hear?
. Which case do we hear?
It turns out we hear ![]() as two separate tones (Eq. (4.4))
whenever the side bands are resolved by the ear. As
mentioned in §4.1.2,
the ear performs a ``short time Fourier analysis'' of incoming sound
(the basilar membrane in the cochlea acts as a mechanical
filter bank). The
resolution of this filterbank--its ability to discern two
separate spectral peaks for two sinusoids closely spaced in
frequency--is determined by the
critical bandwidth of hearing
[44,74,85]. A critical
bandwidth is roughly 15-20% of the band's center-frequency, over most
of the audio range [69]. Thus, the side bands in
sinusoidal AM are heard as separate tones when they are both in the
audio range and separated by at least one critical bandwidth. When
they are well inside the same critical band, ``beating'' is heard. In
between these extremes, near separation by a critical-band, the
sensation is often described as ``roughness'' [28].
as two separate tones (Eq. (4.4))
whenever the side bands are resolved by the ear. As
mentioned in §4.1.2,
the ear performs a ``short time Fourier analysis'' of incoming sound
(the basilar membrane in the cochlea acts as a mechanical
filter bank). The
resolution of this filterbank--its ability to discern two
separate spectral peaks for two sinusoids closely spaced in
frequency--is determined by the
critical bandwidth of hearing
[44,74,85]. A critical
bandwidth is roughly 15-20% of the band's center-frequency, over most
of the audio range [69]. Thus, the side bands in
sinusoidal AM are heard as separate tones when they are both in the
audio range and separated by at least one critical bandwidth. When
they are well inside the same critical band, ``beating'' is heard. In
between these extremes, near separation by a critical-band, the
sensation is often described as ``roughness'' [28].