"You should write a video poker game," Ted said, and I did. A programming partnership was born. Ted continued to supply me with low-level graphics functions, and I continued to write games to test them out. Sometimes I would get ahead of him and ask for more functions, like video-to-video blits. Other times, Ted passed me by and then I would be hard-pressed to think up a new game to use his discoveries.
One day, Ted discovered how to resize video memory in Mode X. This was pure power. I didn't know how to use this feature at first even though it was certainly something to brag about. That's the problem with great inventions. Unless you can find a practical application, it is just another quirk in the system, interesting only to computer nerds. Eventually, though, I found an application for Ted's discovery. As other gamers before me had learned, it is just the perfect thing to use in a tile-based scrolling game. We are about to examine the theory behind the scrolling, and the basis of this technique is Ted's resizeable video memory in Mode X.
Scrolling is a fundamental part of the game we'll be working on in the later chapters. I'm introducing it now because we'll also be using it in the game editor.The next development tool we'll discuss is a level editor. We'll use the level editor to build and modify levels. Of course, the level editor must be able to scroll the entire level if it's going to be useful to us. To understand the level editor, we must first understand the the theory behind tile-based scrolling. The scrolling code that I'll be presenting in this chapter is from the LEVEL.C source file used to build the game editor. Although we'll be exploring this file in detail in the next chapter, we'll look at some of the scrolling code in this chapter so that you can see how the scrolling concepts are implemented. If some of the material confuses you a little, don't worry, it will become clearer as we dissect the level editor in the next chapter. The type of scrolling used in the level editor is slightly less complicated than the scrolling used in the game itself. For example, we don't need to perform diagonal scrolling. We also don't need to scroll in one-pixel increments, although we can. All we'll need for the level editor is simple two-directional scrolling. So this is a good place to start. When we are ready to do the game scrolling in Chapter 11, we'll add more features to the scrolling technique we are introducing now.
The first thing we need to do to scroll our level art is initialize the video mode. This is the same wonderful Mode X video mode we discussed in the previous chapter. But now we are going to do something new with it. We are going to resize it. Mode X allows for four pages of video memory on any VGA card, only don't think of it in that way. Rather than four pages of video memory, try to think of it as one continuous block of video memory. We'll take control of this video memory and reshape it to suit our needs. The way we do this is by initializing video memory and calling a few Fastgraph functions as shown here:
fg_setmode(20); fg_resize(352,744);
Notice that we first set the video mode to Mode X by calling the Fastgraph fg_setmode() function thatwe introduced this function in Chapter 4. Then we call fg_resize().
fg_resize()
The fg_resize() function changes the dimensions of a video page in EGA, VGA, and SVGA graphics modes.
void fg_resize(int width, int height);
* width specifies the new video page width in pixels.
* height specifies the new video page height in pixels.
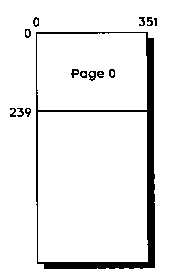
The call to fg_resize() creates a big block of video memory that is 352 pixels wide and 744 pixels high, as shown in Figure 5.1. Video memory has now been resized to a single large rectangle. Inside is the part of video memory that represents the screen--a smaller (320x200 pixels) visible rectangle, also shown in Figure 5.1. The visible rectangle can be located anywhere within the larger rectangle.
Figure 5.1 Resizing video memory to one big rectangle.
We can divide up video memory any way we want, and how we use this video memory is going to be critical to both our game editor and the actual game we develop later in this book. Let's examine the thought process that goes into designing the use of video memory. Think of yourself as a mathematician or an engineer. Get out a piece of graph paper, a ruler, and a calculator. Now ask yourself, "What is the optimal use of this big chunk of video memory?"
Let's start by assigning an area for the visible screen to reside. We need to find a good place to put it, and leave enough room for it so that nothing else gets in its way. We have already decided we are going to need tiles in our game. Experience has shown 16x16 tiles are a good size. On a regular 320x200 screen, you have enough room to fit 20 of them in the horizontal direction, and 12-1/2 in the vertical direction. Hmmm... 12-1/2? That is going to present a problem. We are going to have some overlap in the vertical direction. Better plan a space on your paper that is at least half a tile longer than 200 lines. So the height of our page needs to be at least 208 lines. But is this enough? What if we want to scroll up and down in one-pixel increments? We better leave enough room for a tile at the top and a tile at the bottom. So our page height is going to be 15 tiles high, with 12-1/2 tiles visible at any one time. We'll also have a couple of extra rows of tiles to give us some room to scroll around in. The formula works out like this:
12.5 rows of tiles always visible, round up to 13
+ an extra row of tiles at the top to scroll up + 1
+ an extra row of tiles at the bottom to scroll down + 1
---
total rows of tiles: 15
sixteen rows of pixels per tile x16
---
total height of our page in pixels 240
Therefore, the size of the page we will have to rebuild each frame is 240 pixels; we'll reserve an area this size at the top of our rectangle of video memory and call it page 0, as shown in Figure 5.2.

Figure 5.2 240 rows of pixels reserved in video memory.
The top area will always be a page. We won't use that part of video memory for anything else. The actual visible screen will fit somewhere in this page and will float around as required by the scrolling. We will begin by putting the visible screen right in the middle, at x = 16, y = 16, as shown in Figure 5.3.
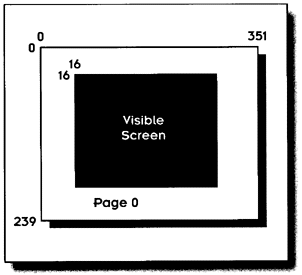
Figure 5.3 The visible screen is located in page 0.
The visible screen is 320x200 pixels and can be located anywhere inside of page 0. It floats easily in this area. All we need is a single call to Fastgraph's fg_pan() function:
fg_pan(screen_orgx, screen_orgy);
The fg_pan() function changes the screen origin (the upper-left corner of the screen) to the specified screen space coordinates.
void fg_pan(int ix, int iy);*ix is the new screen space x coordinate for the screen origin.
*iy is the new screen space y coordinate for the screen origin.
We've introduced two variables here called screen_orgx and screen_orgy. These variables represent the (x,y) coordinates of the origin of the screen in video memory. Since we'll need to refer to them often, we'll make them global variables and declare them like this:
int screen_orgx, screen_orgy;
We begin with screen_orgx = 16 and screen_orgy = 16, as shown in Figure 5.3. Throughout our discussion, we'll assume that screen_orgx and screen_orgy are constrained to the following values:
0 <= screen_orgx < 32 0 <= screen_orgy < 40
If screen_orgx is greater than 31, or screen_orgy is greater than 39, our visible screen will overflow the space we allocated for the page, and we'll see garbage around the edges of the screen. You don't want that to happen! Allowing the visible screen to overflow the edges of the page is like taking a trip into the Twilight Zone. You never quite know what will appear over the horizon. It is an experience best avoided. So we will limit the origin of our visible page to a small area, called the panning area, as shown in Figure 5.4.
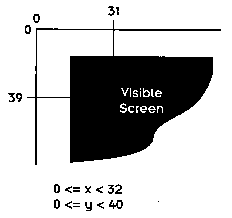
Figure 5.4 Page 0 panning limits.
Notice that screen_orgx and screen_orgy must be less than 32 and 40, respectively. That is, they can have a maximum value of 31 and 39. The reason is obvious: We start counting pixels at 0, so the range from 0 to 31 is 32 pixels, or exactly two tiles.
By now, it should also be obvious why we chose the value 352 as the width of our video memory rectangle. The visible screen is 320 pixels across, which is 20 tiles. We need to leave room for one tile on the left for scrolling left, and another tile on the right for scrolling to the right, so our page needs to be 22 tiles wide; 22 tiles times 16 pixels per tile is 352.
Is one tile all around the edge of the screen all the scrolling room we need? Most scrolling games allow us to move more than 16 pixels in any direction. But what is going to happen to us when we try to move the screen out of the panning area? The answer is, we will need to redraw the screen with new tiles on it. For best results, we'll want to draw the new screen in offscreen video memory. This is going to take some more room. In fact, we're going to need another whole page. Let's put it underneath the first page, and call it page 1, as shown in Figure 5.5.
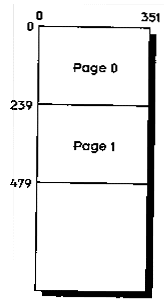
Figure 5.5 Page 1, located beneath page 0.
Notice that page 1 is exactly the same size and shape as page 0. Now that we have two pages, we can alternate between them, in a technique known as page flipping. Our version of page flipping might be a little different than the page flipping you may be familiar with. Physically, video memory is all the same page. All we are doing is moving from one area of video memory to another using fg_pan(). But at this low level, there is really no difference between our technique and conventional page flipping. Both involve changing the starting address of display memory. Resizing video memory to one page simply gives us a little more control over the process. In addition to flipping from one page to the other, we can also control just where on the page we flip to.
Page 1 gives us the panning area shown in Figure 5.6.
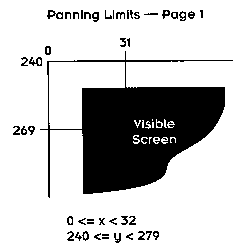
Figure 5.6 Page 1 panning limits.
If the visible screen is at (16,16) on page 0, the same screen will be at (16,256) on page 1. In other words, page 1 is just page 0 with 240 added to the y coordinate.
To simplify things, we will define a variable called yoffset. This variable will be equal to either 0 or 240 depending on whether we are currently displaying page 0 or page 1. Every time we flip pages, all we have to do is change the value of yoffset, as shown in Figure 5.7.
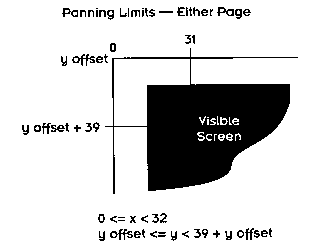
Figure 5.7 Change the value of yoffset when flipping pages.
In our game, we will flip pages quite often--usually between 10-25 frames per second. In fact, we will define one frame of animation to mean a sequence ending in a page flip. Every time we flip pages, we will move the visible screen from page 0 to page 1, or vice versa. We will do this by updating the value of yoffset, and then calling fg_pan():
yoffset = 240 - yoffset; fg_pan(screen_orgx,screen_orgy+yoffset);
This function performs a very fast update of the screen (approximately as fast as the rate of the vertical refresh).
Toggling a Variable
To toggle a variable between two numbers, subtract the current value of the variable from the sum of the numbers. For example, if you want to toggle x between 0 and 1, you could write this code
if (x == 0) x = 1; else x = 0;
which has exactly the same effect as this much shorter bit of code:
x = 1-x;
At this point, let's introduce the concept of the hidden and visual pages. The page that is currently hosting the screen is called the visual page. The other page is the hidden page. In our game, page 0 and page 1 will be constantly alternating roles (10-25 times per second, as I said earlier). Screen updates are always done to the hidden page, then the pages are flipped, and the hidden page becomes the visual page. We then immediately update the new hidden page in anticipation of the next page flip. These updates and page flips continue as long as the program is running. Even when the program appears to be doing nothing (for example when all our sprites are standing perfectly still), we are still flipping pages at approximately 25 frames per second. In the level editor, scrolling works slightly different. We do not need to animate at the same high speed as in the game, so we will not be constantly flipping pages; we only need to flip a page when the level has scrolled out of the viewing area.
As we work through the scrolling code, we will find it convenient to keep track of a little more information. The swap() function updates all the variables that define the hidden and visual pages. The vpo (visual page offset) variable is the same as yoffset. Knowing the bottom of the visual page, as well as the top and the bottom of the hidden page, will be useful to us later. We could always calculate these values "on the fly," but since we will be using them several times per frame and we are interested in saving time, we will compute them once in the swap() function and store them in globals. Then we can have access to them when we need them:
void swap()
{
vpo = 240 - vpo; /* visual page offset */
vpb = vpo + 239; /* visual page bottom */
hpo = 240 - hpo; /* hidden page offset */
hpb = hpo + 239; /* hidden page bottom */
/* set the origin to the visual page */
fg_pan(screen_orgx,screen_orgy+vpo);
}
After the swap() function updates the variables, it calls fg_pan() to do the page flip.
Page 0 and page 1 will almost always be very similar. Most of the time, they will contain the same tiles. There are 15 rows of 22 tiles on page 0, and the same 15 rows of 22 tiles on page 1. The only time when the two pages do not match is when one of the coordinates scrolls outside of the panning limits.
Let's imagine our character is walking east. We want to scroll the screen to the right, continuously and slowly. We will increment the x coordinate one pixel each frame:
screen_orgx = 16;
screen_orgy = 16;
do
{
fg_pan(screen_orgx,screen_orgy+vpo)
screen_orgx++;
}
while (screen_orgx < 32);
We are now at the limit of our panning area. We can't continue on like this. We have to do something! But what?
What we need to do is rebuild the hidden page with all the tiles shifted to the left by one column, and then recalculate the x coordinate to match the new set of tiles.
Suppose we number our columns from 0 to 21, as shown in Figure 5.8. To scroll the picture to the right, we simply need to shift all the tiles of columns to the left. It's that easy. All we need to do is copy the tiles from the last 21 columns of the visual page to the first 21 columns of the hidden page, like this:
fg_transfer(16,251,vpo,vpb, 0,hpb, 0,0);
After the transfer, the columns on the hidden page look like Figure 5.9.
Figure 5.8 Columns numbered from 0 to 21.
Figure 5.9 22 columns of tiles on the hidden page.
The large rectangular area from 16 to 351 on the visual page has been copied to the area from 0 to 336 on the hidden page. Column 0 is gone; it's been covered up by column 1, and all the other columns have been shifted to the left. Column 21 is duplicated. We don't really need two copies of column 21 on the hidden page; what we need is the next column of tiles (column 22). We call the appropriate function to blit the tiles to column 22.
Now our hidden page looks like Figure 5.10.
Figure 5.10 Updating the hidden page.
This is exactly what we wanted. But we are not quite ready to complete the frame yet. We need to adjust the x coordinate before we do the page flip. Since all the visual elements of the screen have effectively been moved 16 pixels to the left, we need to decrement the x coordinate by 16 as well:
screen_orgx -= 16; fg_pan(screen_orgx,screen_orgy+yoffset);
The frame is complete. We have moved one more pixel to the right; now we can keep scrolling right and we won't have to do redraw the screen again for 15 more pixels.
The scrolling technique will be most useful if we write a function to handle various cases. The scroll_right() function in the level editor source file, LEVEL.C, looks like this:
int scroll_right(int npixels)
{
register int i;
/* no tiles need to be redrawn */
if (screen_orgx <= 32-npixels)
{
screen_orgx+=npixels;
fg_pan(screen_orgx,screen_orgy);
}
/* redraw one column of tiles and do a page swap */
else if (tile_orgx < ncols - 22)
{
tile_orgx++;
screen_orgx-=(16-npixels);
fg_transfer(16,351,vpo,vpo+239,0,hpo+239,0,0);
swap();
for(i = 0; i< 15; i++)
put_tile(21,i);
}
/* can't scroll right */
else return(ERR);
return(OK);
}
The scroll_right() function allows us to pass a variable number of pixels and handles three cases:
Usually, our scrolling background is going to have more than 22 columns and 15 rows. In fact, it will have many, many more. We need to start thinking in tile space. Tile space is a coordinate system based on rows and columns of tiles. Since each tile is 16x16 pixels, conversions from tile space to pixels usually involve subtracting the origin and multiplying by 16. Similarly, converting from pixels coordinates in video memory to tile space will require dividing by 16 and adding the origin.
Just as the visible screen floats in the visual page, the visual page floats within the tile space. This concept is illustrated in Figure 5.11.
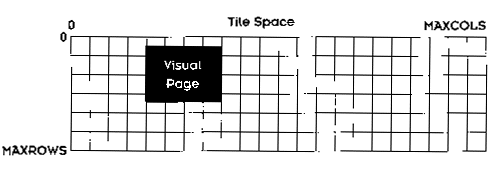
Figure 5.11 The visible page floats within the available tile space.
Tile space is a huge map, stretching 240 tiles long and 200 tiles high. The visual page can be located anywhere in this tile space, occupying only 22 columns and 15 rows at a time. The shaded part in the Figure 5.11 represents the visual page. Remember, the screen is smaller than the visual page by about two tiles in the x and y directions. So as the screen floats freely in the visual page, and the visual page floats in the tile space, and the illusion of scrolling is accomplished.
Just as the origin of the screen must stay within the panning limits, the origin of the visual page must stay within some limits too. We can not let the visual page scroll off the edge of the tile map in any direction. The smallest value for tile_orgx is 0, and the largest value is MAXCOLS - 22. Similarly, the smallest value for tile_orgy is 0 and the largest value is MAXROWS - 15. We will test for these limits in our scrolling function. If we meet or exceed the tile limits, then we have reached the end of the world and are unable to scroll any further.
Now let's look at how we built those columns of tiles. Each column has 16 tiles. But where do the tiles come from? The best place to store tiles is in some area of video memory where nothing else is happening. Since we have already defined areas for page 0 and page 1, let's look at Figure 5.12 to see what we have left.
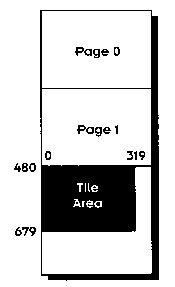
Figure 5.12 Video memory.
The shaded area is as good a place as any to put the tiles. We'll allocate an area 320x200 pixels for this function. Let's call this the tile area; we'll plan on not using this for anything else.
Let's take a closer look at the tile area. As you can see in Figure 5.13, there are 240 unique tiles, numbered from 0 to 239: Their location in the tile area determines their number. Tile number 0 is in the upper-left corner, tile number 239 is in the lower-right corner, and all the other tiles are in between.
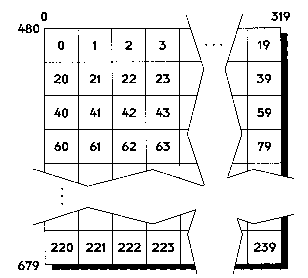
Figure 5.13 A closer look at the tile area.
All the backgrounds in our game are constructed from some combination of these tiles. The tiles are simply copied from the tile area to the hidden page using a straight video memory-to-video memory blit. The function to copy the tile from the tile area to the hidden page looks like this:
void put_tile(int column, int row){
int tile_num;
int x,y;
int x1,x2,y1,y2;
/* get the tile information from the tile map */
tile_num = (int)level_map[column+tile_orgx][row+tile_orgy];
/* calculate the destination coordinates */
x = column * 16;
y = row * 16 + 15 + hpo;
/* calculate the source coordinates */
x1 = (tile_num%20)*16; x2 = x1+15;
y1 = (tile_num/20)*16 + tpo;
y2 = y1+15;
/* copy the tile */
fg_transfer(x1,x2,y1,y2,x,y,0,0);
}
This function calculates the tile number based on the row and column destination, then it finds the location of the tile number in the tile area. It also calculates the destination in pixels. Finally, the rectangular area is copied from the tile area to the correct position on the hidden page.
This function also introduces some new global variables, and before we go any further, let's define them. First, tile_orgx is the x origin in tile space. That is, it is the number of the first column. In our previous example, before the screen scrolled, tile_orgx was 0. After the scroll, it was 1. Similarly, tile_orgy defines the row coordinate at the top of the page, also called the y origin.
The put_tile() function makes it very easy to define another useful function, redraw_screen(). The redraw_screen() function builds a whole screen, one tile at a time:
void redraw_screen (void)
{
register int i, j;
for (i=0; i<22; i++)
{
for (j=0; j<15; j++)
{
put_tile (i,j);
}
}
}
The tile information that defines the background is stored in the array level_map. This is a two dimensional array defined like this:
unsigned char far level_map[MAXCOLS][MAXROWS]; We can use this array to define some very large levels. Suppose we want our level map to be 240 tiles wide and 240 tiles high. This will give us a total of 48,000 tiles, as shown here:
240 columns x 200 rows ------------- 48,000 tiles
It is easy to see why we use a char (byte) array instead of an integer array. If this was an integer array instead, we would quickly overflow a 64K segment boundary. However, defining this as an unsigned char array means each tile must have a value less than or equal to 254. This isn't a problem because, as illustrated earlier, we have exactly 240 unique tiles. That was certainly good planning! Isn't it nice how this works out?
240 columns and 200 rows actually defines a huge area. Remember, each tile has 256 pixels (16x16). Or in other words:
240 columns x 16 = 3840 pixels horizontally x 200 rows x 16 = 3200 pixels vertically ------------- ----- 48,000 tiles x256 = 12,288,000 pixels total
That's over 12 million pixels! Yet, amazingly, we're keeping all this information in one 48K array, as well as within the tile area in video memory.
The way we can do this, of course, is by duplicating a lot of information. If our game calls for 20 windows, what we'll actually have is one window repeated 20 times. Small trees and big trees are composed of the same branches organized in different ways. One blue tile can be repeated infinitely for an apparently endless sky. Think of your level map as the whole world. The rows and columns are the coordinate system that keep track of it, and the tiles themselves define what it looks like.
Vertical scrolling is accomplished in approximately the same way as horizontal scrolling. The y coordinate is incremented (or decremented) until it is outside the panning limits. Then a large area, missing a row either from the top or the bottom, is copied from the visual page to the hidden page. The missing row is added at the top or bottom as needed, and the page flip completes the frame. Here is the function for the scrolling part of the frame:
int scroll_up(int npixels)
{
register int i;
/* no tiles need to be redrawn */
if (screen_orgy >= npixels)
{
screen_orgy-=npixels;
fg_pan(screen_orgx,screen_orgy);
}
/* redraw one row of tiles and do a page swap */
else if (tile_orgy > 0)
{
tile_orgy--;
screen_orgy+=(16-npixels);
fg_transfer(0,351,vpo,223+vpo,0,hpo+239,0,0);
for(i = 0; i< 22; i++)
put_tile(i,0);
swap();
}
else /* can't scroll up */
return(-1);
return(OK);
}
You should now have a good grasp of how scrolling works. Once you can visualize the various coordinate systems and the page flipping and scrolling techniques, the other functions will fall easily into place. Be sure you have a clear understanding of the concepts discussed in this chapter before continuing. As we said before, this chapter is the foundation for the rest of our game engine, and is at the very heart of the side-scrolling arcade game technology. In case you were wondering about whether I am currently ahead of Ted in finding uses for the technology he develops, I am afraid I am not. He is most decidedly ahead of me. He has developed Fastgraph to run in 32-bit flat model protected mode and he wants me to write code to make use of virtual bitmaps many megabytes in size. Talk about raw power! I haven't the foggiest idea what to do with all this new stuff. But something will come to me . . . eventually.
Cover |
Contents |
Downloads
Fastgraph Home Page |
books |
Magazine Reprints
Copyright © 1998 Ted Gruber Software Inc. All Rights Reserved.
Awards |
Acknowledgements |
Introduction
Chapter 1 |
Chapter 2 |
Chapter 3 |
Chapter 4 |
Chapter 5 |
Chapter 6
Chapter 7 |
Chapter 8 |
Chapter 9 |
Chapter 10 |
Chapter 11 |
Chapter 12
Chapter 13 |
Chapter 14 |
Chapter 15 |
Chapter 16 |
Chapter 17 |
Chapter 18
Appendix |
License Agreement |
Glossary |
Installation Notes |
Home Page
So you want to be a Computer Game Developer